Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

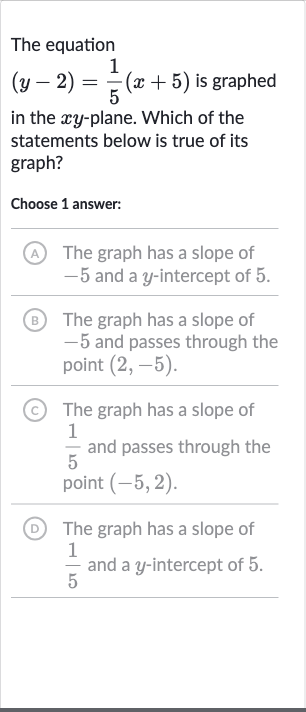
The equation (y-2)=(1)/(5)(x+5) is graphed in the xy-plane. Which of the statements below is true of its graph? Choose 1 answer: (A) The graph has a slope of -5 and a y-intercept of 5 . (B) The graph has a slope of -5 and passes through the point (2,-5). (C) The graph has a slope of (1)/(5) and passes through the point (-5,2). (D) The graph has a slope of (1)/(5) and a y-intercept of 5 .

The equation\newline(y−2)=15(x+5)(y-2)=\frac{1}{5}(x+5) is graphed in the xyxy-plane. Which of the statements below is true of its graph?\newlineChoose 11 answer:\newline(A) The graph has a slope of −5-5 and a yy-intercept of 55.\newline(B) The graph has a slope of −5-5 and passes through the point (2,−5)(2,-5).\newline(C) The graph has a slope of 15\frac{1}{5} and passes through the point (−5,2)(-5,2).\newline(D) The graph has a slope of 15\frac{1}{5} and a yy-intercept of 55.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 8right chevron icon
Write a linear equation from a slope and y-interceptright chevron icon

Full solution

Q. The equation\newline(y−2)=15(x+5)(y-2)=\frac{1}{5}(x+5) is graphed in the xyxy-plane. Which of the statements below is true of its graph?\newlineChoose 11 answer:\newline(A) The graph has a slope of −5-5 and a yy-intercept of 55.\newline(B) The graph has a slope of −5-5 and passes through the point (2,−5)(2,-5).\newline(C) The graph has a slope of 15\frac{1}{5} and passes through the point (−5,2)(-5,2).\newline(D) The graph has a slope of 15\frac{1}{5} and a yy-intercept of 55.
  1. Identify Equation Form: Identify the slope-intercept form of the equation.\newlineThe slope-intercept form of a linear equation is y=mx+by = mx + b, where mm is the slope and bb is the y-intercept.
  2. Rewrite in Slope-Intercept Form: Rewrite the given equation in slope-intercept form.\newlineStarting with y−2=15(x+5)y-2=\frac{1}{5}(x+5), we add 22 to both sides to isolate yy: y=15(x+5)+2y = \frac{1}{5}(x+5) + 2.
  3. Simplify Equation: Simplify the equation to identify the slope and y-intercept.\newlineWe can distribute the (1)/(5)(1)/(5) across (x+5)(x+5) to get y=(1)/(5)x+(1)/(5)⋅5+2y = (1)/(5)x + (1)/(5)\cdot5 + 2. Simplifying further, we get y=(1)/(5)x+1+2y = (1)/(5)x + 1 + 2, which simplifies to y=(1)/(5)x+3y = (1)/(5)x + 3.
  4. Identify Slope: Identify the slope from the simplified equation.\newlineThe coefficient of xx in the equation y=15x+3y = \frac{1}{5}x + 3 is 15\frac{1}{5}, which is the slope of the line.
  5. Identify Specific Point: Identify a specific point through which the graph passes.\newlineThe equation was initially given as (y−2)=15(x+5)(y-2)=\frac{1}{5}(x+5). Setting xx to −5-5, we get (y−2)=15(−5+5)(y-2)=\frac{1}{5}(-5+5), which simplifies to (y−2)=0(y-2)=0. Adding 22 to both sides gives us y=2y = 2. Therefore, when x=−5x = -5, y=2y = 2, which means the graph passes through the point (−5,2)(-5, 2).
  6. Choose Correct Statement: Choose the correct statement based on the identified slope and point.\newlineThe graph has a slope of (15)(\frac{1}{5}) and passes through the point (−5,2)(-5, 2), which corresponds to option (C).

More problems from Write a linear equation from a slope and y-intercept

Question
Does the point (0,4)(0, 4) satisfy the equation y=xy = x??
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the slope of the line y=−4x+25 y = -4x + \frac{2}{5} .
Get tutor helpright-arrow

Posted 5 months ago

Question
Rewrite the following equation in slope-intercept form.\newliney+8=−8(x−10)y + 8 = -8(x - 10)
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the y y -intercept of the line 14x−16y=−10 14x - 16y = -10 .\newlineWrite your answer as an integer or decimal or fraction, not as an ordered pair.
Get tutor helpright-arrow

Posted 5 months ago

Question
Line q q has a slope of −23 \frac{-2}{3} . Line r r is perpendicular to q q . What is the slope of line r r ?
Get tutor helpright-arrow

Posted 5 months ago

Question
Find the slope of the line y+3=−118(x+6)y + 3 = -\frac{1}{18}(x + 6).\newline
Get tutor helpright-arrow

Posted 5 months ago

Question
Line p p has an equation of y=−8x+6 y = -8x + 6 . Line q q , which is perpendicular to line p p , includes the point (2,−2) (2, -2) . What is the equation of line q q ??\newlineWrite the equation in slope-intercept form.
Get tutor helpright-arrow

Posted 5 months ago

Question
Is the graph of this equation a horizontal or vertical line?\newlinex=7x = 7
Get tutor helpright-arrow

Posted 5 months ago

Question
Determine the standard form of the following equation:\newliney=−10x+7 y = -10x + 7
Get tutor helpright-arrow

Posted 5 months ago

Question
A line with a slope of 99 passes through the point (9,9)(9,9). What is its equation in point-slope form?
Get tutor helpright-arrow

Posted 5 months ago

View all (39)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant