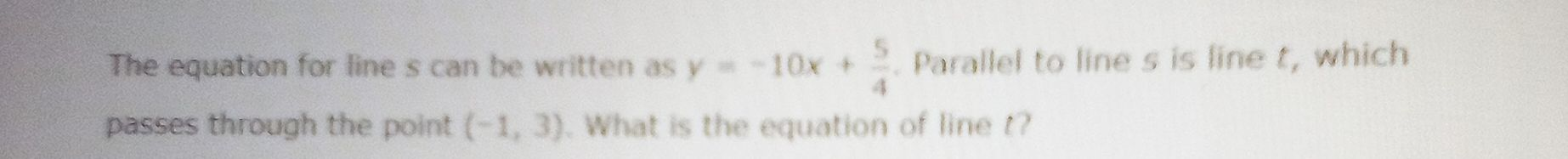The equation for line s can be written as y=-10 x+(5)/(4). Parallel to line 5 is line t, which passes through the point (-1,3). What is the equation of line 1 ?

Question

The equation for line  s can be written as  y=-10 x+(5)/(4). Parallel to line 5 is line  t, which passes through the point  (-1,3). What is the equation of line 1 ?

Bytelearn · Accepted Answer

Determine slope of line s: Determine the slope of line s. The equation of line s is given as y = -10x + 5/4. The slope of a line in the form y = mx + b is m, where m is the coefficient of x. The slope of line s is -10.Find slope of line t: Since line t is parallel to line s, it must have the same slope. Parallel lines have identical slopes. Therefore, the slope of line t is also -10.Use point-slope form: Use the point-slope form to find the equation of line t. The point-slope form of a line is y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line. We know the slope (m) is -10 and the point (x1, y1) is (-1, 3).Plug slope and point: Plug the slope and point into the point-slope form to get the equation of line t. y - 3 = -10(x - (-1)) y - 3 = -10(x + 1)Simplify equation: Simplify the equation to get it into slope-intercept form, y = mx + b. y - 3 = -10x - 10 y = -10x - 10 + 3 y = -10x - 7

The equation for line $s$ can be written as $y=-10 x+\frac{5}{4}$ . Parallel to line $5$ is line $t$ , which passes through the point $(-1,3)$ . What is the equation of line $1$ ?

Full solution

More problems from Write an equation for a parallel or perpendicular line

Related topics

The equation for line s s s can be written as y=−10x+54 y=-10 x+\frac{5}{4} y=−10x+45​. Parallel to line 555 is line t t t, which passes through the point (−1,3) (-1,3) (−1,3). What is the equation of line 111 ?

The equation for line $s$ can be written as $y=-10 x+\frac{5}{4}$ . Parallel to line $5$ is line $t$ , which passes through the point $(-1,3)$ . What is the equation of line $1$ ?