Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The circumference of a hula hoop is 86 picm. What is the radius of the hula hoop? cm

The circumference of a hula hoop is 86πcm 86 \pi \mathrm{cm} .\newlineWhat is the radius of the hula hoop?\newline□\square cm \mathrm{cm}

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Geometryright chevron icon
Find measures of complementary, supplementary, vertical, and adjacent anglesright chevron icon

Full solution

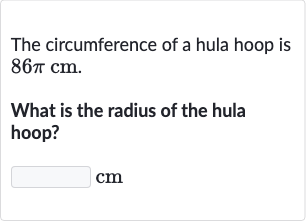
Q. The circumference of a hula hoop is 86πcm 86 \pi \mathrm{cm} .\newlineWhat is the radius of the hula hoop?\newline□\square cm \mathrm{cm}
  1. Circle Circumference Formula: We know the formula for the circumference of a circle is C=2πrC = 2\pi r, where CC is the circumference and rr is the radius.
  2. Given Circumference: We have the circumference, C=86 picmC = 86\,\text{picm}. We need to find the radius, rr.
  3. Rearranging Formula: Rearrange the formula to solve for rr: r=C2πr = \frac{C}{2\pi}.
  4. Substitute Circumference: Plug in the given circumference: r=86 picm2π.r = \frac{86 \, \text{picm}}{2\pi}.
  5. Calculate Radius: Calculate the radius: r≈862×3.14r \approx \frac{86}{2 \times 3.14}. This is approximately 866.28\frac{86}{6.28}.
  6. Final Result: Do the division: r≈13.69r \approx 13.69 picm.

More problems from Find measures of complementary, supplementary, vertical, and adjacent angles

Question
Classify the pair of angles. Tr\newlineThe angles are complementar
Get tutor helpright-arrow

Posted 19 days ago

Question
f(3)=(3)2+6(3)−16(3)2−4(3)−12 f(3)=\frac{(3)^{2}+6(3)-16}{(3)^{2}-4(3)-12}
Get tutor helpright-arrow

Posted 19 hours ago

Question
h(x)=−5+(−4)+20 h(x)=-5+\sqrt{(-4)+20}
Get tutor helpright-arrow

Posted 19 hours ago

Question
g(x)=4(3)2+5(3)2 g(x)=\frac{4(3)^{2}+5}{(3)^{2}}
Get tutor helpright-arrow

Posted 19 hours ago

Question
4545) m∠EFC m \angle E F C
Get tutor helpright-arrow

Posted 19 hours ago

Question
f(x)=2∣(−3)−2∣ f(x)=2|(-3)-2|
Get tutor helpright-arrow

Posted 19 hours ago

Question
\begin{tabular}{|c|c|}\newline\hline(y+3)2−x=36 (y+3)^{2}-x=36 & ◯ \bigcirc Function \quad Not a function \\\newline\hliney−9x2=4 y-9 x^{2}=4 & ◯ \bigcirc Function ◯ \quad \bigcirc Not a function \\\newline\hliney=∣x+3 y=\mid x+3 & ◯ \bigcirc Function \quad Not a function \\\newline\hline 5x+y=7 5 \sqrt{x}+y=7 & ◯ \bigcirc Function ◯ \quad \bigcirc Not a function \\\newline\hline\newline\end{tabular}
Get tutor helpright-arrow

Posted 19 hours ago

Question
\begin{tabular}{|c|lc|}\newline\hline(y+3)2−x=36 (y+3)^{2}-x=36 & ○ Function & O Not a function \\\newline\hliney−9x2=4 y-9 x^{2}=4 & ○ Function & ○ Not a function \\\newline\hliney=∣x+3∣ y=|x+3| & ○ Function & O Not a function \\\newline\hline 5x+y=7 5 \sqrt{x}+y=7 & ○ Function & O Not a function \\\newline\hline\newline\end{tabular}
Get tutor helpright-arrow

Posted 19 hours ago

Question
f(x+h)−f(x)h \frac{f(x+h)-f(x)}{h} for f(x)=x2+2x f(x)=x^{2}+2 x
Get tutor helpright-arrow

Posted 19 hours ago

Question
In 20162016, the city of Rio de Janeiro had a population density of 377377 people\text{people}/km2\text{km}^{2}. What was the population density of Rio de Janeiro in people per square meter? people\text{people}/m2\text{m}^{2}
Get tutor helpright-arrow

Posted 19 hours ago

View all (2)