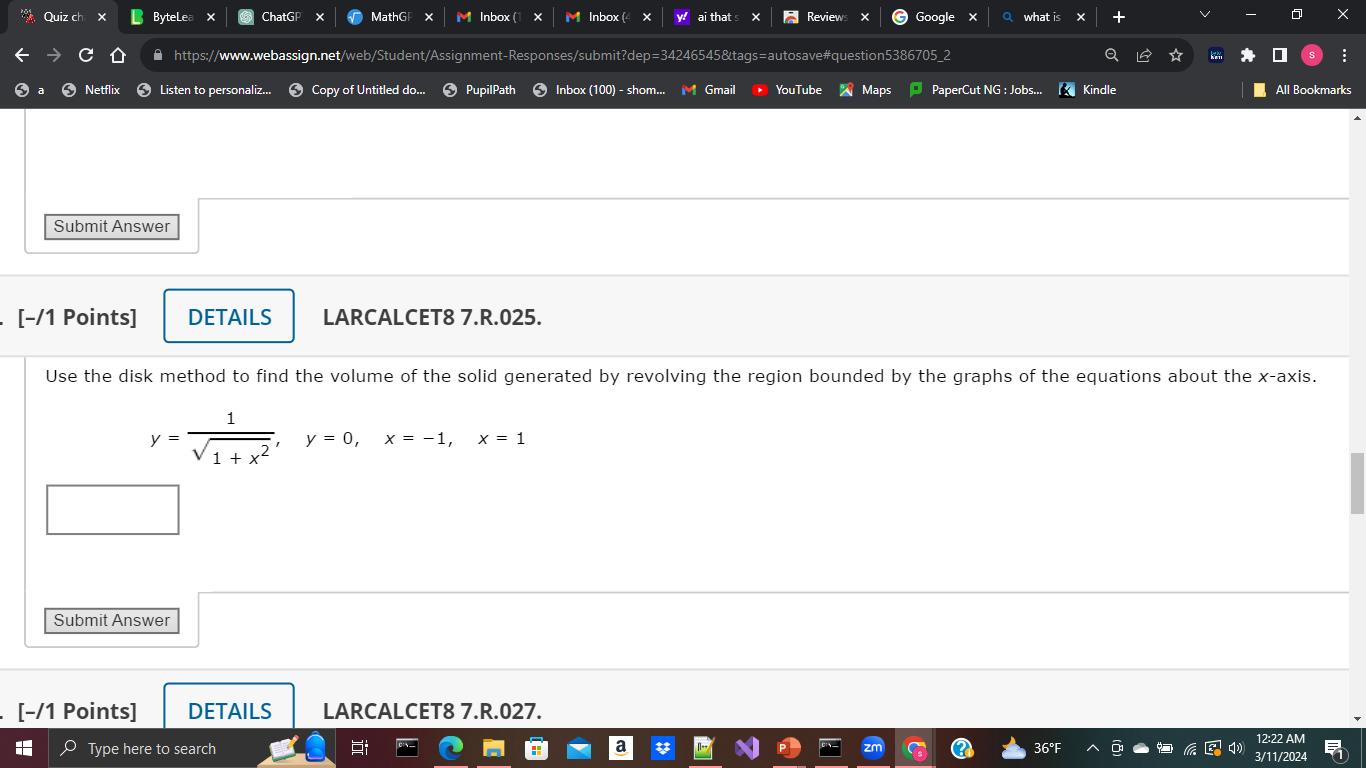
Use the disk method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x-axis. y=(1)/(sqrt(1+x^(2))),quad y=0,quad x=-1,quad x=1

Question

Bytelearn · Accepted Answer

Set up integral: Set up the integral for the volume using the disk method. The volume V of a solid of revolution generated by revolving a region about the x-axis can be found using the formula: $$ V = \pi \int_{a}^{b} [f(x)]^2 dx $$ where $ f(x) $ is the function that defines the upper boundary of the region being revolved, and $ a $ and $ b $ are the limits of integration along the x-axis. For the given problem, $ f(x) = \frac{1}{\sqrt{1+x^2}} $, $ a = -1 $, and $ b = 1 $. So, the integral to find the volume is: $$ V = \pi \int_{-1}^{1} \left(\frac{1}{\sqrt{1+x^2}}\right)^2 dx $$Simplify integrand: Simplify the integrand before integrating. The integrand simplifies to: $$ \left(\frac{1}{\sqrt{1+x^2}}\right)^2 = \frac{1}{1+x^2} $$ So the integral becomes: $$ V = \pi \int_{-1}^{1} \frac{1}{1+x^2} dx $$Integrate function: Integrate the function. The integral of $ \frac{1}{1+x^2} $ is $ \arctan(x) $, so we have: $$ V = \pi \left[ \arctan(x) \right]_{-1}^{1} $$Evaluate integral: Evaluate the integral from $ a = -1 $ to $ b = 1 $. $$ V = \pi \left[ \arctan(1) - \arctan(-1) \right] $$ Since $ \arctan(1) = \frac{\pi}{4} $ and $ \arctan(-1) = -\frac{\pi}{4} $, we have: $$ V = \pi \left[ \frac{\pi}{4} - (-\frac{\pi}{4}) \right] $$ $$ V = \pi \left[ \frac{\pi}{4} + \frac{\pi}{4} \right] $$ $$ V = \pi \left[ \frac{\pi}{2} \right] $$ $$ V = \frac{\pi^2}{2} $$

Use the disk method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the $x$ -axis. $\newline$ $y=\frac{1}{\sqrt{1+x^{2}}}, \quad y=0, \quad x=-1, \quad x=1$

Full solution

More problems from One-step inequalities: word problems

Related topics

Use the disk method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the x x x-axis.\newliney=11+x2,y=0,x=−1,x=1 y=\frac{1}{\sqrt{1+x^{2}}}, \quad y=0, \quad x=-1, \quad x=1 y=1+x2​1​,y=0,x=−1,x=1

Use the disk method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the $x$ -axis. $\newline$ $y=\frac{1}{\sqrt{1+x^{2}}}, \quad y=0, \quad x=-1, \quad x=1$