Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

State all integer values of
x in the interval
-3 <= x <= 4 that satisfy the following inequality:

3x+10 >= 4
Answer:
x=

State all integer values of $x$ in the interval $-3 \leq x \leq 4$ that satisfy the following inequality: $\newline$ $3 x+10 \geq 4$ $\newline$ Answer: $x=$

View step-by-step help

View step-by-step help

Solve quadratic inequalities

Full solution

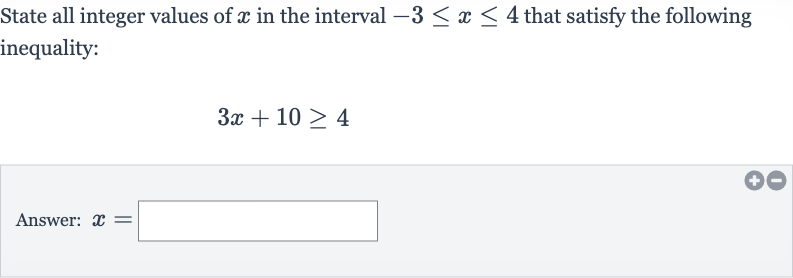
Q. State all integer values of

x

in the interval

-3 \leq x \leq 4

that satisfy the following inequality:

\newline

3 x+10 \geq 4

\newline

Answer:

x=

Solve Inequality for x: First, we need to solve the inequality $3x + 10 \geq 4$ for $x$ . $\newline$ Subtract $10$ from both sides of the inequality to isolate the term with $x$ . $\newline$ $3x + 10 - 10 \geq 4 - 10$ $\newline$ $3x \geq -6$
Divide by $3$ : Next, divide both sides of the inequality by $3$ to solve for $x$ . $\frac{3x}{3} \geq \frac{-6}{3}$ $x \geq -2$
Find Integer Values: Now we have the inequality $x \geq -2$ . We need to find all integer values of $x$ that satisfy this inequality within the interval $-3 \leq x \leq 4$ . $\newline$ Since $-2$ is within the interval, we start from $-2$ and list all integers up to $4$ . $\newline$ The integers are $-2$ , $-1$ , $0$ , $1$ , $x$ $0$ , $x$ $1$ , $4$ .

More problems from Solve quadratic inequalities

Question

s

\newline

|s| + 3 \geq 8

Posted 4 months ago

Question

Which compound inequality represents the value of

x ?

\newline

(x - 1)(x + 1) > 0

\newline

Posted 4 months ago

Question

A particular company charges advertisers a one time cost of

\$500

, in addition to

\$4.50

for every one thousand times an advertisement is shown on the company's webpage. An advertiser wants its ad to appear

M

thousand times on the webpage, but does not want to spend more than

\$5,000

. Which of the following inequalities best describes the situation?

\newline

\newline

500+4.50M\geq5,000

\newline

4.50+500M>5,000

\newline

500+4.50M\leq5,000

\newline

500+4.50M<5,000

Posted 7 months ago

Question

7x+1 < x+9

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x > \frac{4}{3}

\newline

x < \frac{4}{3}

\newline

x < 1

\newline

x < \frac{5}{3}

Posted 4 months ago

Question

52-3x < -14

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x > -\frac{38}{3}

\newline

x > \frac{38}{3}

\newline

x < 22

\newline

x > 22

Posted 10 months ago

Question

5-3x > 2x+2

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

x < \frac{7}{5}

\newline

x < 3

\newline

x < \frac{3}{5}

\newline

x > \frac{3}{5}

Posted 10 months ago

Question

Rani is a real estate agent. For each house she sells, she pays

\$ 100

in fees, but earns a commission of

1.8 \%

of the selling price of the house. Rani's total profit from a particular house is

\$ 4,580

p

represents the selling price of the house, which equation best models the situation?

\newline

1

\newline

0.018 p-100=4580

\newline

0.018 p+100=4580

\newline

(100-0.018) p=4580

\newline

(100+0.018) p=4580

Posted 8 months ago

Question

A commercial airplane that is

1

500

2

500

-mile journey is traveling at

450

knots in still air when it picks up a tailwind of

150

knots (in the same direction). If

h

is the number of hours remaining in the airplane's flight, which of the following equations best describes the situation?

\newline

1

\mathrm{knot}=1.15

miles per hour (mph)

\newline

1

\newline

1,500+690 h=2,500

\newline

1,500+600 h=2,500

\newline

1,500-600 h=2,500

\newline

1,500-690 h=2,500

Posted 7 months ago

Question

A weeping willow that is

15

feet in height grows to a maximum height of

35

y

years at a constant rate of

24

inches per year. Which of the following equations best describes this situation?

\newline

1

=12

\newline

1

\newline

35=15+2 y

\newline

35=15+24 y

\newline

35=15-2 y

\newline

35=15-24 y

Posted 10 months ago

Question

The gas mileage for a car is

23

miles per gallon when the car travels at

60

miles per hour. The car begins a trip with

13

gallons in its tank, travels at an average speed of

60

miles per hour for

h

hours, and ends the trip with

10

gallons in its tank. Which of the following equations best models this situation?

\newline

1

\newline

13-\frac{23 h}{60}=10

\newline

13-\frac{60 h}{23}=10

\newline

\frac{13-60 h}{23}=10

\newline

\frac{13-23 h}{60}=10

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant