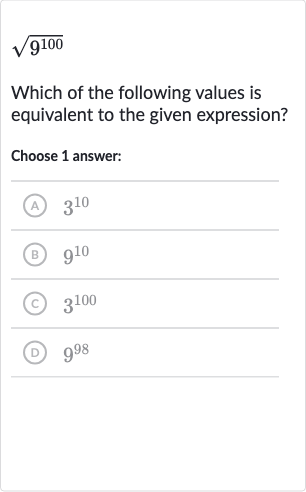
sqrt(9^(100)) Which of the following values is equivalent to the given expression? Choose 1 answer: (A) 3^(10) (B) 9^(10) (c) 3^(100) (D) 9^(98)

Question

sqrt(9^(100)) Which of the following values is equivalent to the given expression? Choose 1 answer: (A)  3^(10) (B)  9^(10) (c)  3^(100) (D)  9^(98)

Bytelearn · Accepted Answer

Rewriting the expression: We are given the expression sqrt(9^(100)). The square root of a number is the same as raising that number to the power of 1/2. Therefore, we can rewrite the expression as (9^(100))^(1/2).Simplifying using exponent properties: Using the property of exponents that states (a^m)^n = a^(m*n), we can simplify the expression further. In this case, we have a = 9, m = 100, and n = 1/2.Further simplification: Multiplying the exponents, we get 9^(100 * 1/2) which simplifies to 9^(50).Rewriting using exponent properties: We know that 9 is 3 squared, or 9 = 3^2. Therefore, we can rewrite 9^(50) as (3^2)^(50).Multiplying the exponents: Using the property of exponents again, we multiply the exponents 2 and 50 to get (3^2)^(50) = 3^(2*50).Calculating the exponent: Calculating 2*50 gives us 100, so we have 3^(2*50) = 3^(100).Final equivalent value: Therefore, the equivalent value of the expression sqrt(9^(100)) is 3^(100), which corresponds to option (C).

$\sqrt{9^{100}}$ $\newline$ Which of the following values is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $3^{10}$ $\newline$ (B) $9^{10}$ $\newline$ (C) $3^{100}$ $\newline$ (D) $9^{98}$

Full solution

More problems from Relationship between squares and square roots

Related topics

9100 \sqrt{9^{100}} 9100​\newlineWhich of the following values is equivalent to the given expression?\newlineChoose 111 answer:\newline(A) 310 3^{10} 310\newline(B) 910 9^{10} 910\newline(C) 3100 3^{100} 3100\newline(D) 998 9^{98} 998

$\sqrt{9^{100}}$ $\newline$ Which of the following values is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $3^{10}$ $\newline$ (B) $9^{10}$ $\newline$ (C) $3^{100}$ $\newline$ (D) $9^{98}$