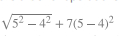AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Full solution
Q.
- Calculate Inside Square Root: We need to evaluate the expression step by step. First, we will calculate the value inside the square root, which is .So,
- Take Square Root: Now we take the square root of the result from the previous step.
- Evaluate Parentheses: Next, we evaluate the second part of the expression, which is . First, calculate the value inside the parentheses: .
- Raise to Power: Now we raise the result to the power of : .
- Multiply Result: Then we multiply the result by : .
- Add Final Results: Finally, we add the results of the square root and the multiplication together to get the final answer.
