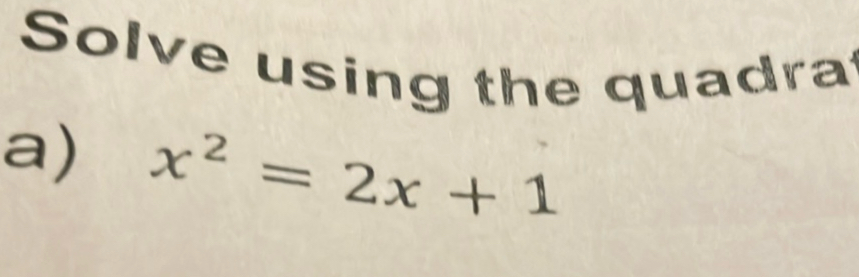Solve using the quadra a) x^(2)=2x+1

Question

Solve using the quadra a)  x^(2)=2x+1

Bytelearn · Accepted Answer

Write Standard Quadratic Form: Write the equation in standard quadratic form. To find the roots of the equation, we need to write it in the form ax^2 + bx + c = 0. Subtract 2x and 1 from both sides to get the equation in standard form. x^2 - 2x - 1 = 0Identify Coefficients: Identify the coefficients a, b, and c. In the equation x^2 - 2x - 1 = 0, the coefficients are: a = 1, b = -2, c = -1Use Quadratic Formula: Use the quadratic formula to find the roots. The quadratic formula is given by (-b ± sqrt(b^2 - 4ac)) / (2a). Substitute the values of a, b, and c into the formula. (-(-2) ± sqrt((-2)^2 - 4*1*(-1))) / (2*1)Simplify Square Root: Simplify the expression under the square root. Calculate the discriminant (b^2 - 4ac). (-2)^2 - 4*1*(-1) = 4 + 4 = 8Substitute Discriminant: Substitute the discriminant back into the quadratic formula. (2 ± sqrt(8)) / 2Divide by 2: Simplify the square root of 8. sqrt(8) can be written as sqrt(4*2), which simplifies to 2*sqrt(2). (2 ± 2*sqrt(2)) / 2Write Roots in Simplest Form: Simplify the expression by dividing by 2. Divide both terms in the numerator by 2. 1 ± sqrt(2)Write the roots in simplest form. The roots of the equation are: x = 1 + sqrt(2) and x = 1 - sqrt(2)

Solve using the quadra $\newline$ a) $x^{2}=2 x+1$

Full solution

More problems from Quadratic equation with complex roots

Related topics

Solve using the quadra\newlinea) x2=2x+1 x^{2}=2 x+1 x2=2x+1

Solve using the quadra $\newline$ a) $x^{2}=2 x+1$