Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve the following equation for
x. Express your answer in the simplest form.

5(3x+3)=5(3x+3)

Solve the following equation for $x$ . Express your answer in the simplest form. $\newline$ $5(3 x+3)=5(3 x+3)$ $\newline$

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

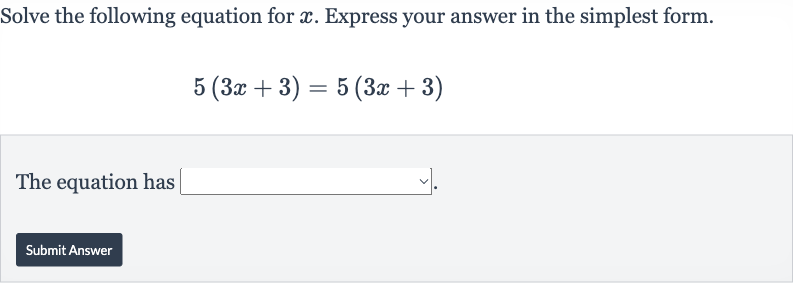
Q. Solve the following equation for

x

. Express your answer in the simplest form.

\newline

5(3 x+3)=5(3 x+3)

\newline

Simplify Equation: First, we need to simplify both sides of the equation if possible. $\newline$ $5(3x + 3) = 5(3x + 3)$ $\newline$ Since both sides of the equation are identical, they simplify to the same expression.
Distribute $5$ : We can distribute the $5$ on both sides of the equation. $\newline$ $5 \times 3x + 5 \times 3 = 5 \times 3x + 5 \times 3$ $\newline$ This simplifies to: $\newline$ $15x + 15 = 15x + 15$
Subtract $15x$ : Next, we subtract $15x$ from both sides of the equation to try to isolate $x$ .
$15x + 15 - 15x = 15x + 15 - 15x$
This simplifies to:
$15 = 15$
Verify Identity: We notice that the variable $x$ has been eliminated, and we are left with a statement that $15$ equals $15$ , which is always true. $\newline$ This means that the equation is an identity and is true for all values of $x$ .
Infinite Solutions: Since the equation is true for all values of $x$ , there is no single solution for $x$ . Instead, $x$ can be any real number.

More problems from Find the roots of factored polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 2 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 1 month ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 2 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 2 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 2 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 2 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 2 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 2 months ago