Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve the equation x^(2)-7x+8=0 to the nearest tenth. Answer: x=

Solve the equation x2−7x+8=0 x^{2}-7 x+8=0 to the nearest tenth.\newlineAnswer: x= x=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Solve exponential equations using logarithmsright chevron icon

Full solution

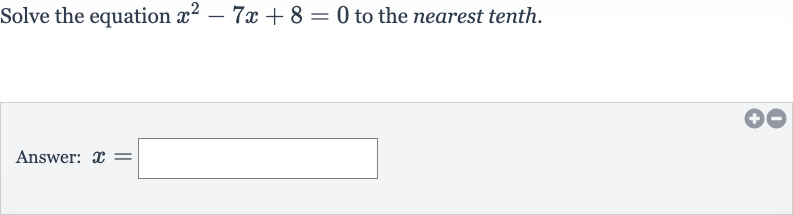
Q. Solve the equation x2−7x+8=0 x^{2}-7 x+8=0 to the nearest tenth.\newlineAnswer: x= x=
  1. Identify Equation Type: Identify the type of equation.\newlineWe have a quadratic equation in the form of ax2+bx+c=0ax^2 + bx + c = 0, where a=1a = 1, b=−7b = -7, and c=8c = 8.
  2. Solve Using Quadratic Formula: Solve the quadratic equation using the quadratic formula.\newlineThe quadratic formula is x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}.\newlineHere, a=1a = 1, b=−7b = -7, and c=8c = 8.
  3. Calculate Discriminant: Calculate the discriminant b2−4acb^2 - 4ac.\newlineDiscriminant = (−7)2−4(1)(8)=49−32=17(-7)^2 - 4(1)(8) = 49 - 32 = 17.
  4. Apply to Quadratic Formula: Apply the discriminant to the quadratic formula.\newlinex=−(−7)±172⋅1x = \frac{-(-7) \pm \sqrt{17}}{2 \cdot 1}\newlinex=7±172x = \frac{7 \pm \sqrt{17}}{2}
  5. Calculate Possible Solutions: Calculate the two possible solutions for xx.\newlineFirst solution: x=7+172x = \frac{7 + \sqrt{17}}{2}\newlineSecond solution: x=7−172x = \frac{7 - \sqrt{17}}{2}
  6. Evaluate Solutions: Evaluate the solutions to the nearest tenth.\newlineFirst solution: x≈(7+4.123)/2≈11.123/2≈5.6x \approx (7 + 4.123) / 2 \approx 11.123 / 2 \approx 5.6\newlineSecond solution: x≈(7−4.123)/2≈2.877/2≈1.4x \approx (7 - 4.123) / 2 \approx 2.877 / 2 \approx 1.4

More problems from Solve exponential equations using logarithms

Question
Solve. Write your answer as an integer or a fraction in simplest form.\newline5x=15^x=1\newlinex=x= _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Steven opened a savings account and deposited $100.00\$100.00 as principal. The account earns 9%9\% interest, compounded annually. What is the balance after 55 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.\newline$\$____
Get tutor helpright-arrow

Posted 2 months ago

Question
Use the following function rule to find f(1) f(1) .\newlinef(x)=12(7)x+8 f(x) = 12(7)^x + 8 \newlinef(1)= f(1) = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
The town of Valley View conducted a census this year, which showed that it has a population of 1,8001,800 people. Based on the census data, it is estimated that the population of Valley View will grow by 12%12\% each decade.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the town population, yy, xx decades after this census was taken.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=9x7 = 9^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=ex7 = e^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve. Simplify your answer.\newlinelog⁡u=1\log u = 1\newlineu=u = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Simplify your answer.\newline7log⁡x=77\log x = 7\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
How does g(t)=3t g(t) = 3^t change over the interval from t=3 t = 3 to t=4 t = 4 ?\newlineChoices:\newline(A) g(t) g(t) decreases by 3 3 \newline(B) g(t) g(t) increases by 3 3 \newline(C) g(t) g(t) decreases by 3% 3\%\newline(D) g(t) g(t) increases by 200%200\%
Get tutor helpright-arrow

Posted 2 months ago

Question
A function f(x) f(x) increases by 6 6 over every unit interval in x x and f(0)=0 f(0) = 0 .\newlineWhich could be a function rule for f(x) f(x) ?\newlineChoices:\newline(A) f(x)=6xf(x) = 6^x\newline(B) f(x)=6xf(x) = 6x\newline(C) f(x)=16xf(x) = \frac{1}{6^x}\newline(D) f(x)=x6f(x) = \frac{x}{6}
Get tutor helpright-arrow

Posted 2 months ago

View all (33)