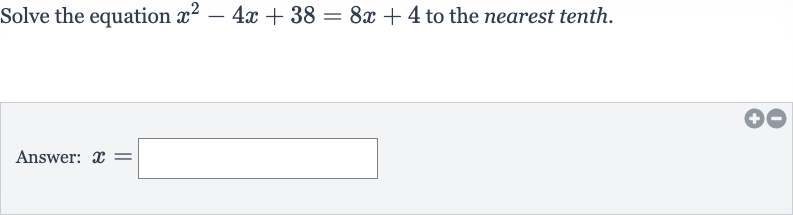
Solve the equation x^(2)-4x+38=8x+4 to the nearest tenth. Answer: x=

Question

Solve the equation  x^(2)-4x+38=8x+4 to the nearest tenth. Answer:  x=

Bytelearn · Accepted Answer

Set Equation Equal to Zero: Bring all terms to one side of the equation to set it equal to zero. x^2 - 4x + 38 = 8x + 4 x^2 - 4x - 8x + 38 - 4 = 0 x^2 - 12x + 34 = 0Use Quadratic Formula: Use the quadratic formula to solve for x. The quadratic formula is x = [-b ± sqrt(b^2 - 4ac)] / (2a), where a = 1, b = -12, and c = 34.Calculate Discriminant: Calculate the discriminant (b^2 - 4ac) to determine the nature of the roots. Discriminant = (-12)^2 - 4(1)(34) Discriminant = 144 - 136 Discriminant = 8 Since the discriminant is positive, there are two real solutions.Calculate Solutions: Calculate the two solutions using the quadratic formula. x = [-(-12) ± sqrt(8)] / (2*1) x = [12 ± sqrt(8)] / 2Simplify Square Root: Simplify the square root of the discriminant to the nearest tenth. sqrt(8) ≈ 2.8 (to the nearest tenth)Finalize Solutions: Calculate the two values of x using the simplified square root. x = (12 + 2.8) / 2 and x = (12 - 2.8) / 2 x ≈ 14.8 / 2 and x ≈ 9.2 / 2 x ≈ 7.4 and x ≈ 4.6

Solve the equation $x^{2}-4 x+38=8 x+4$ to the nearest tenth. $\newline$ Answer: $x=$

Full solution

More problems from Solve multi-step equations with fractional coefficients

Related topics

Solve the equation x2−4x+38=8x+4 x^{2}-4 x+38=8 x+4 x2−4x+38=8x+4 to the nearest tenth.\newlineAnswer: x= x= x=

Solve the equation $x^{2}-4 x+38=8 x+4$ to the nearest tenth. $\newline$ Answer: $x=$