AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
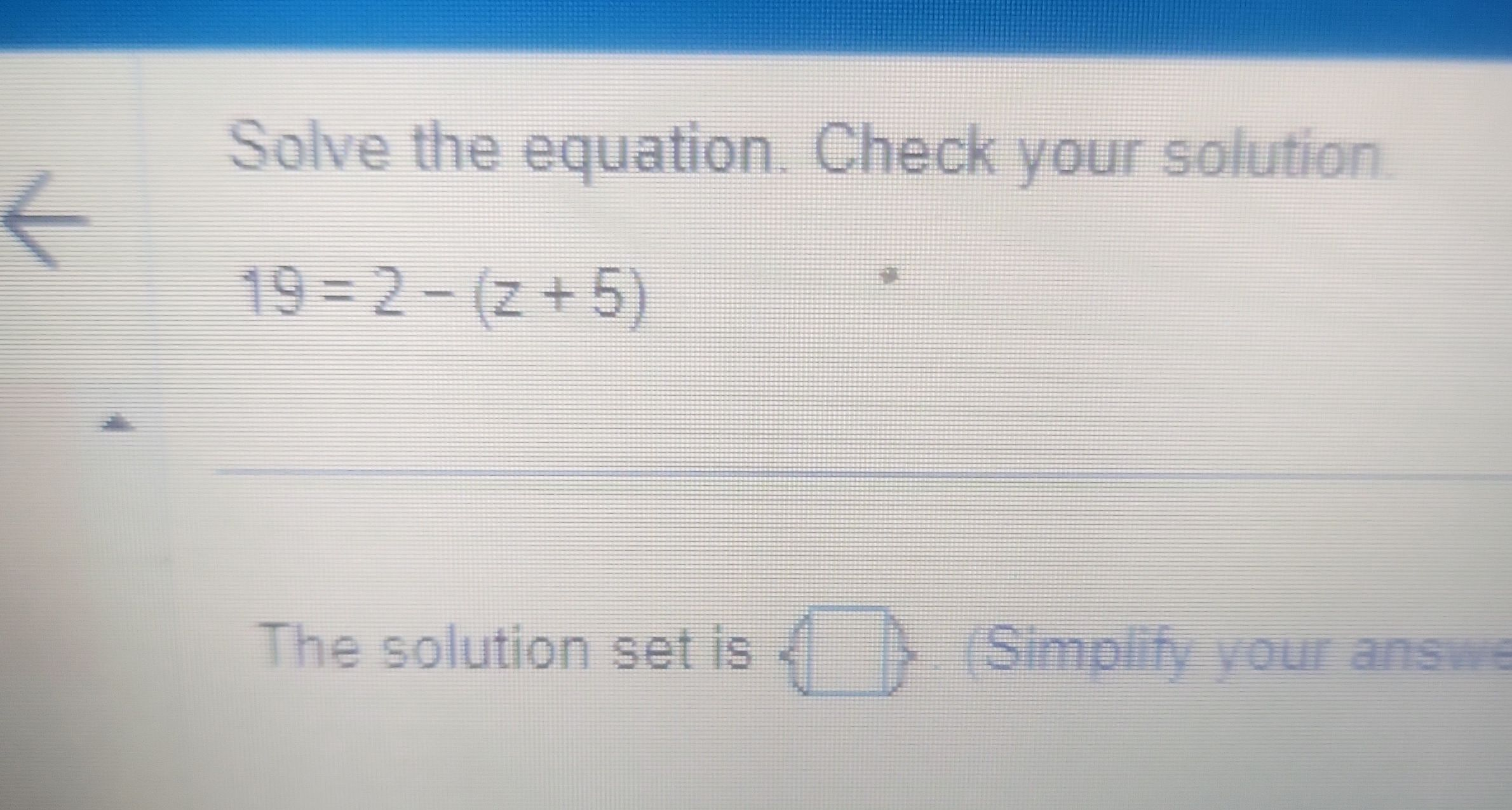
Solve the equation. Check your solution.The solution set is (Type an integer or a simplified fraction).
Full solution
Q. Solve the equation. Check your solution.The solution set is (Type an integer or a simplified fraction).
- Isolate variable : First, we need to isolate the variable on one side of the equation. We start by adding to both sides of the equation to move the term involving to the left side.Calculation: becomes
- Combine like terms: Next, we simplify the left side of the equation by combining like terms.Calculation: becomes
- Subtract : Now, we subtract from both sides of the equation to solve for .Calculation: becomes
- Check solution: Finally, we check our solution by substituting back into the original equation to see if both sides are equal.Calculation: becomes which simplifies to
