Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for x, rounding to the nearest hundredth. 10^(x)=68 Answer:

Solve for x x , rounding to the nearest hundredth.\newline10x=68 10^{x}=68 \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Precalculusright chevron icon
Solve exponential equations using logarithmsright chevron icon

Full solution

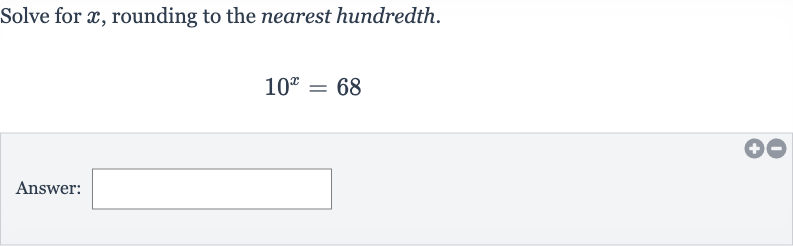
Q. Solve for x x , rounding to the nearest hundredth.\newline10x=68 10^{x}=68 \newlineAnswer:
  1. Write Equation to Solve: Write down the equation that needs to be solved.\newlineWe have the equation 10x=6810^{x} = 68.\newlineWe need to solve for xx.
  2. Apply Logarithm: Apply the logarithm to both sides of the equation to solve for xx. Taking the logarithm base 1010 of both sides, we get log⁡(10x)=log⁡(68)\log(10^{x}) = \log(68).
  3. Simplify Using Logarithm Property: Simplify the equation using the property of logarithms that log⁡(ab)=blog⁡(a)\log(a^b) = b\log(a). This gives us xlog⁡(10)=log⁡(68)x\log(10) = \log(68). Since log⁡(10)\log(10) is 11, the equation simplifies to x=log⁡(68)x = \log(68).
  4. Calculate Log Value: Calculate the value of log⁡(68)\log(68) using a calculator.x=log⁡(68)≈1.83250891270624x = \log(68) \approx 1.83250891270624
  5. Round to Nearest Hundredth: Round the value of xx to the nearest hundredth.x≈1.83x \approx 1.83

More problems from Solve exponential equations using logarithms

Question
Solve. Write your answer as an integer or a fraction in simplest form.\newline5x=15^x=1\newlinex=x= _____
Get tutor helpright-arrow

Posted 2 months ago

Question
Steven opened a savings account and deposited $100.00\$100.00 as principal. The account earns 9%9\% interest, compounded annually. What is the balance after 55 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.\newline$\$____
Get tutor helpright-arrow

Posted 2 months ago

Question
Use the following function rule to find f(1) f(1) .\newlinef(x)=12(7)x+8 f(x) = 12(7)^x + 8 \newlinef(1)= f(1) = _____
Get tutor helpright-arrow

Posted 1 month ago

Question
The town of Valley View conducted a census this year, which showed that it has a population of 1,8001,800 people. Based on the census data, it is estimated that the population of Valley View will grow by 12%12\% each decade.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the town population, yy, xx decades after this census was taken.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=9x7 = 9^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=ex7 = e^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
Solve. Simplify your answer.\newlinelog⁡u=1\log u = 1\newlineu=u = ____
Get tutor helpright-arrow

Posted 2 months ago

Question
Solve. Simplify your answer.\newline7log⁡x=77\log x = 7\newlinex=x = ____
Get tutor helpright-arrow

Posted 1 month ago

Question
How does g(t)=3t g(t) = 3^t change over the interval from t=3 t = 3 to t=4 t = 4 ?\newlineChoices:\newline(A) g(t) g(t) decreases by 3 3 \newline(B) g(t) g(t) increases by 3 3 \newline(C) g(t) g(t) decreases by 3% 3\%\newline(D) g(t) g(t) increases by 200%200\%
Get tutor helpright-arrow

Posted 2 months ago

Question
A function f(x) f(x) increases by 6 6 over every unit interval in x x and f(0)=0 f(0) = 0 .\newlineWhich could be a function rule for f(x) f(x) ?\newlineChoices:\newline(A) f(x)=6xf(x) = 6^x\newline(B) f(x)=6xf(x) = 6x\newline(C) f(x)=16xf(x) = \frac{1}{6^x}\newline(D) f(x)=x6f(x) = \frac{x}{6}
Get tutor helpright-arrow

Posted 2 months ago

View all (33)