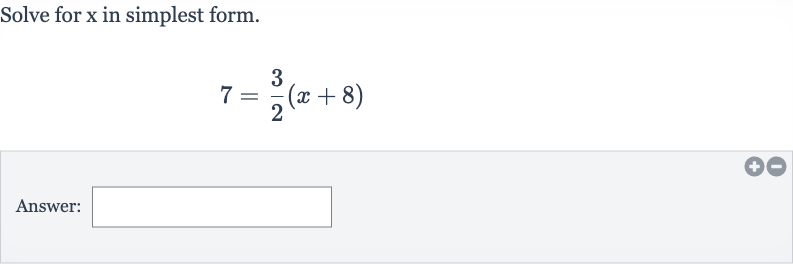AI tutor
Full solution
Q. Solve for in simplest form.Answer:
- Set up equation: First, we need to set up the equation based on the given expression: .
- Isolate x: To solve for x, we need to isolate x on one side of the equation. We can start by multiplying both sides of the equation by the reciprocal of , which is , to cancel out the fraction on the right side.
- Multiply left side: Perform the multiplication on the left side of the equation:
- Cancel fractions: On the right side, the and will cancel each other out, leaving us with:
- Subtract : Now, we need to subtract from both sides to solve for :
- Perform subtraction: To subtract (which is the same as ) from , we perform the subtraction:
- Perform subtraction: To subtract (which is the same as ) from , we perform the subtraction: Perform the subtraction to find the value of :