AI tutor
Full solution
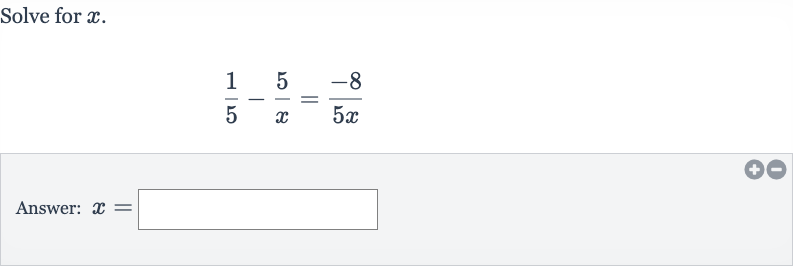
Q. Solve for .Answer:
- Find Common Denominator: Find a common denominator for the terms on the left side of the equation.The common denominator for and is . We will rewrite each fraction with the common denominator .
- Rewrite with Common Denominator: Rewrite the equation with the common denominator. becomes and becomes . The equation now looks like this:
- Combine Fractions: Combine the fractions on the left side of the equation.Since they have the same denominator, we can combine the numerators:
- Equate Numerators: Since the denominators on both sides of the equation are the same, we can equate the numerators.
- Solve for x: Solve for x by adding to both sides of the equation.