AI tutor
Full solution
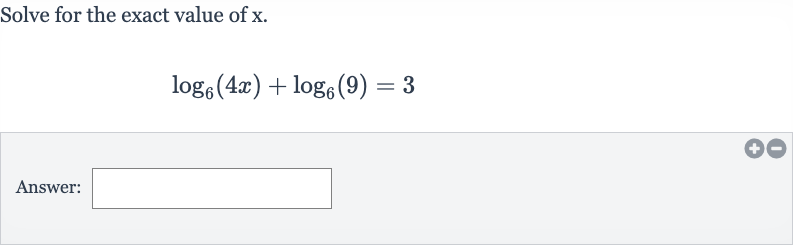
Q. Solve for the exact value of .Answer:
- Apply product rule of logarithms: Apply the product rule of logarithms to combine the two logarithmic terms.The product rule of logarithms states that .Therefore, becomes .
- Simplify expression: Simplify the expression inside the logarithm.Multiplying by gives us .So, simplifies to .
- Set equal to : Set the simplified logarithmic expression equal to . We now have the equation .
- Convert to exponential form: Convert the logarithmic equation to its exponential form.The exponential form of is .So, .
- Calculate value of : Calculate the value of . equals .So, we have .
- Solve for x: Solve for x by dividing both sides of the equation by .Dividing by gives us .
- Calculate exact value of x: Calculate the exact value of . divided by equals . So, .