AI tutor
Full solution
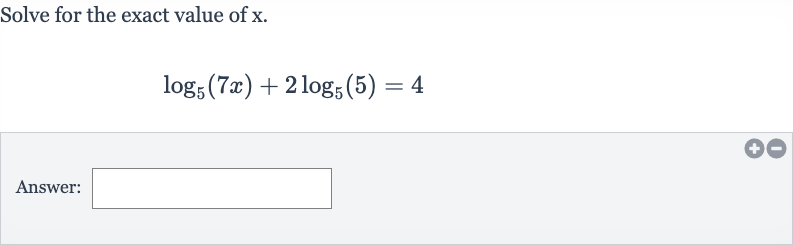
Q. Solve for the exact value of .Answer:
- Apply Power Rule: Apply the power rule of logarithms to simplify the second term.The power rule of logarithms states that . can be rewritten as .Calculation: .
- Substitute Simplified Term: Substitute the simplified second term back into the equation.The equation now becomes .
- Apply Product Rule: Apply the product rule of logarithms to combine the two logarithmic terms.The product rule states that .Combine the terms: .Calculation: .
- Convert to Exponential Form: Convert the logarithmic equation to its exponential form.The exponential form of is .Convert the equation: .Calculation: .
- Solve for x: Solve for x.Divide both sides of the equation by to isolate .Calculation: .Calculation: (This is a repeating decimal, so we can express it as a fraction).Calculation: .