AI tutor
Full solution
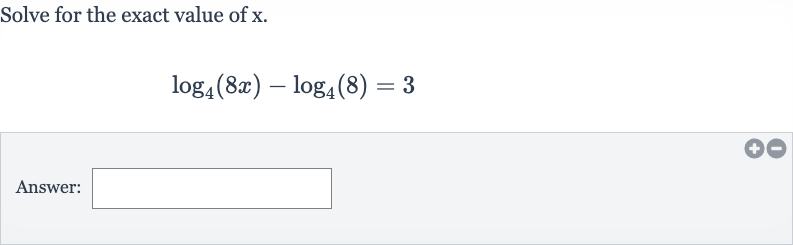
Q. Solve for the exact value of .Answer:
- Combine logarithms: Apply the quotient rule of logarithms to combine the two logarithms into one.Quotient rule of logarithms: Simplify the fraction inside the logarithm.
- Simplify fraction: Set the combined logarithm equal to . Now, we need to rewrite this logarithmic equation in exponential form.Calculate the value of .
- Set equal to : Solve for .