AI tutor
Full solution
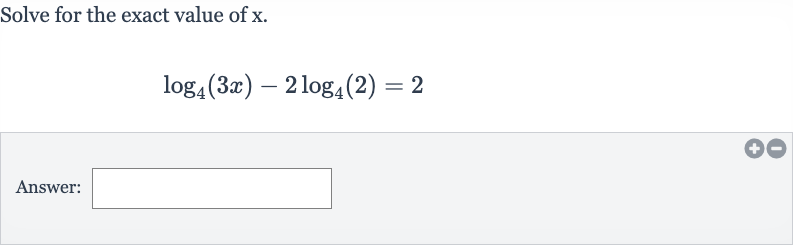
Q. Solve for the exact value of .Answer:
- Apply Power Rule: Let's start by applying the power rule of logarithms to the term with the coefficient of .Power rule of logarithm:
- Rewrite Equation: Now, we rewrite the equation using the result from the power rule.
- Combine Logarithmic Terms: Next, we apply the quotient rule of logarithms to combine the logarithmic terms on the left side.Quotient rule of logarithm:
- Convert to Exponential Form: To solve for , we need to rewrite the logarithmic equation in exponential form.
- Solve for x: Now, we solve for by multiplying both sides of the equation by and then dividing by .