AI tutor
Full solution
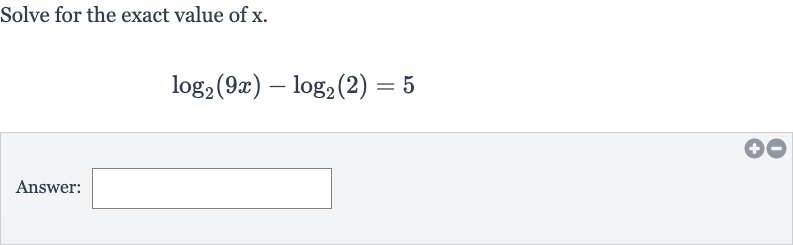
Q. Solve for the exact value of .Answer:
- Apply Quotient Rule: Apply the quotient rule of logarithms to combine the two logarithmic expressions into one.Quotient rule of logarithm:
- Use Logarithm Property: Rewrite the equation using the property of logarithms that states if , then . implies
- Calculate and Solve: Calculate and solve for ., so
- Isolate : Multiply both sides of the equation by to isolate on one side.
- Divide by : Divide both sides of the equation by to solve for .