AI tutor
Full solution
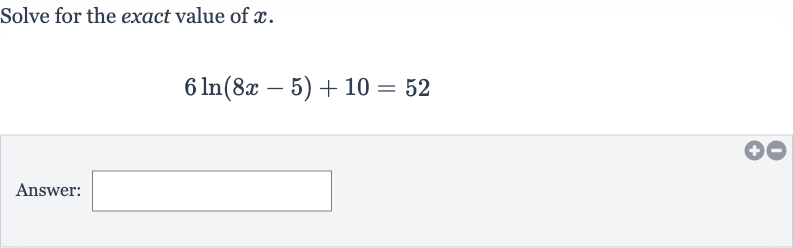
Q. Solve for the exact value of .Answer:
- Isolate natural logarithm term: First, isolate the natural logarithm term by subtracting from both sides of the equation.
- Divide by : Next, divide both sides of the equation by to solve for the natural logarithm of .
- Exponentiate to remove ln: Now, exponentiate both sides of the equation to remove the natural logarithm, using the property .
- Add to isolate x: Add to both sides of the equation to isolate the term with .
- Divide by to solve for x: Finally, divide both sides by to solve for x.
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help