Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Solve for the exact value of x. 5ln(8x+6)-12=3 Answer:

Solve for the exact value of x x .\newline5ln⁡(8x+6)−12=3 5 \ln (8 x+6)-12=3 \newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Precisionright chevron icon

Full solution

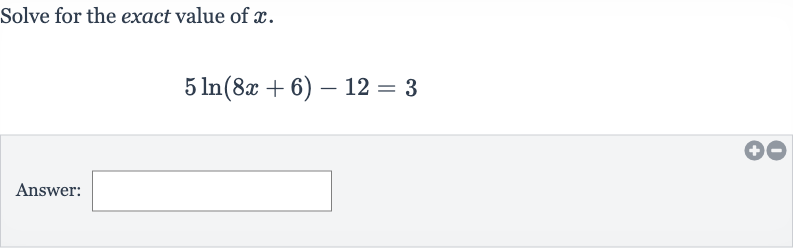
Q. Solve for the exact value of x x .\newline5ln⁡(8x+6)−12=3 5 \ln (8 x+6)-12=3 \newlineAnswer:
  1. Isolate natural logarithm term: Isolate the natural logarithm term.\newlineWe start by adding 1212 to both sides of the equation to isolate the term with the natural logarithm.\newline5ln⁡(8x+6)−12+12=3+125\ln(8x+6) - 12 + 12 = 3 + 12\newline5ln⁡(8x+6)=155\ln(8x+6) = 15
  2. Divide sides to solve: Divide both sides by 55 to solve for the natural logarithm of the expression.\newline5ln⁡(8x+6)5=155 \frac{5\ln(8x+6)}{5} = \frac{15}{5} \newlineln⁡(8x+6)=3 \ln(8x+6) = 3
  3. Exponentiate to remove logarithm: Exponentiate both sides to remove the natural logarithm.\newlineeln⁡(8x+6)=e3e^{\ln(8x+6)} = e^3\newline8x+6=e38x+6 = e^3
  4. Subtract to solve for 8x8x: Subtract 66 from both sides to solve for 8x8x.8x+6−6=e3−68x + 6 - 6 = e^3 - 68x=e3−68x = e^3 - 6
  5. Divide to solve for x: Divide both sides by 88 to solve for x.\newline8x8=e3−68\frac{8x}{8} = \frac{e^3 - 6}{8}\newlinex=e3−68x = \frac{e^3 - 6}{8}

More problems from Precision

Question
A rectangular prism with length ℓ \ell , width w w , and height h h has a volume of ℓwh \ell w h .\newlineWhat is the volume of a prism which has a base of 5 m 5 \mathrm{~m} by 3 m 3 \mathrm{~m} , and a height of 4 m 4 \mathrm{~m} ?\newlinem3 \mathrm{m}^{3}
Get tutor helpright-arrow

Posted 7 months ago

Question
Solve for the exact value of x x .\newline2ln⁡(2x−4)+6=16 2 \ln (2 x-4)+6=16 \newlineAnswer:
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 1616 miles\newline(B) 93.293.2 miles
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 36.636.6 inches\newline(B) 16.5116.51 inches
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 60.7260.72 feet\newline(B) 1919 feet
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 11.45 cm11.45\,\text{cm}\newline(B) 8.6 cm8.6\,\text{cm}
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 61.861.8 pounds\newline(B) 39.0539.05 pounds
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 21 km21\,\text{km}\newline(B) 75.18 km75.18\,\text{km}
Get tutor helpright-arrow

Posted 6 months ago

Question
Which measurement is more precise?\newlineChoices:\newline(A) 53.453.4 teaspoons\newline(B) 24.3324.33 teaspoons
Get tutor helpright-arrow

Posted 6 months ago

Question
An arithmetic sequence j j starts 22,15,… 22,15, \ldots . Explain how you would calculate the value of the 500500th term.
Get tutor helpright-arrow

Posted 1 hour ago

View all (76)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant