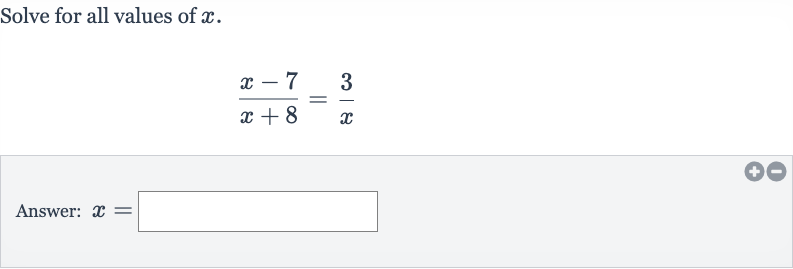
Solve for all values of x. (x-7)/(x+8)=(3)/(x) Answer: x=

Question

Solve for all values of  x.  (x-7)/(x+8)=(3)/(x) Answer:  x=

Bytelearn · Accepted Answer

Cross-multiply fractions: Cross-multiply to eliminate the fractions. (x - 7) * x = 3 * (x + 8)Distribute and simplify: Distribute to simplify both sides of the equation. x^2 - 7x = 3x + 24Move terms and set to zero: Move all terms to one side to set the equation to zero. x^2 - 7x - 3x - 24 = 0 x^2 - 10x - 24 = 0Factor quadratic equation: Factor the quadratic equation. (x - 12)(x + 2) = 0Solve for x: Set each factor equal to zero and solve for x. x - 12 = 0 or x + 2 = 0 x = 12 or x = -2Check for extraneous solutions: Check for extraneous solutions by plugging the values back into the original equation. For x = 12: (12 - 7) / (12 + 8) = 3 / 12 5 / 20 = 3 / 12 1 / 4 = 1 / 4 (True, so x = 12 is a valid solution)  For x = -2: (-2 - 7) / (-2 + 8) = 3 / -2 -9 / 6 = 3 / -2 -3 / 2 = 3 / -2 (True, but x = -2 is not a valid solution because it makes the denominator of the original equation's right side zero)

Solve for all values of $x$ . $\newline$ $\frac{x-7}{x+8}=\frac{3}{x}$ $\newline$ Answer: $x=$

Full solution

More problems from Solve multi-step equations with fractional coefficients

Related topics

Solve for all values of x x x.\newlinex−7x+8=3x \frac{x-7}{x+8}=\frac{3}{x} x+8x−7​=x3​\newlineAnswer: x= x= x=

Solve for all values of $x$ . $\newline$ $\frac{x-7}{x+8}=\frac{3}{x}$ $\newline$ Answer: $x=$