AI tutor
Full solution
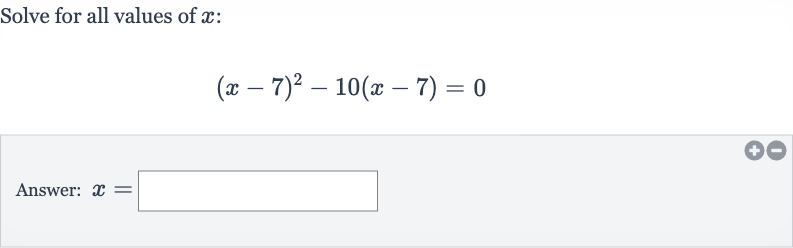
Q. Solve for all values of :Answer:
- Recognize quadratic form: Recognize the quadratic form of the equation.The given equation is in the form of a quadratic equation after expanding the squared term and distributing the .
- Factor common term: Factor the common term from both parts of the equation.This simplifies to:
- Simplify factored equation: Further simplify the factored equation.
- Apply zero-product property: Apply the zero-product property.If the product of two factors is zero, then at least one of the factors must be zero.So, set each factor equal to zero and solve for : or
- Solve for x: Solve each equation for x. => =>
More problems from Composition of linear and quadratic functions: find an equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help