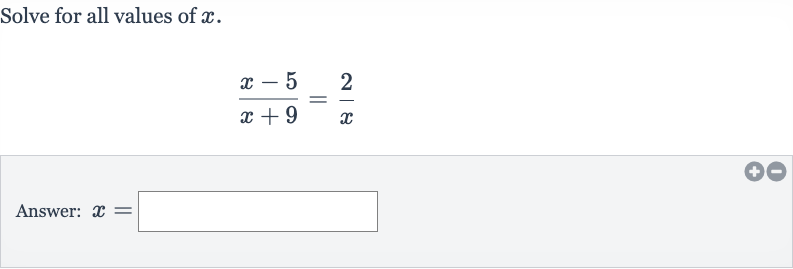
Solve for all values of x. (x-5)/(x+9)=(2)/(x) Answer: x=

Question

Solve for all values of  x.  (x-5)/(x+9)=(2)/(x) Answer:  x=

Bytelearn · Accepted Answer

Find Common Denominator: First, we need to find a common denominator to combine the fractions on both sides of the equation. The common denominator here is x(x+9).Multiply by Common Denominator: Next, we multiply both sides of the equation by the common denominator to eliminate the fractions: x(x+9) * (x-5)/(x+9) = x(x+9) * (2)/(x)Simplify Equation: Simplify the equation by canceling out the common terms on both sides: x(x-5) = 2(x+9)Distribute and Combine Terms: Now, distribute the x on the left side and the 2 on the right side: x^2 - 5x = 2x + 18Set Equation to Zero: Bring all terms to one side to set the equation to zero and combine like terms: x^2 - 5x - 2x - 18 = 0 x^2 - 7x - 18 = 0Factor Quadratic Equation: Factor the quadratic equation: (x - 9)(x + 2) = 0Solve for x: Set each factor equal to zero and solve for x: x - 9 = 0 or x + 2 = 0 x = 9 or x = -2Check Solutions: We must check these solutions to ensure they do not make the original equation undefined by causing division by zero. The original equation has x in the denominator, so x cannot be 0. Also, x cannot be -9 because that would make the denominator of the left side of the original equation zero.Check x = 9: Checking x = 9: (9-5)/(9+9) = (2)/(9) 4/18 = 2/9 2/9 = 2/9 (This is true, so x = 9 is a valid solution.)Check x = -2: Checking x = -2: (-2-5)/(-2+9) = (2)/(-2) -7/7 = -1 -1 = -1 (This is true, but we must remember that x cannot be -2 because it would make the original right side of the equation undefined.)Discard Invalid Solution: Since x = -2 makes the original equation undefined, we discard this solution. The only solution is x = 9.

Solve for all values of $x$ . $\newline$ $\frac{x-5}{x+9}=\frac{2}{x}$ $\newline$ Answer: $x=$

Full solution

More problems from Find the roots of factored polynomials

Related topics

Solve for all values of x x x.\newlinex−5x+9=2x \frac{x-5}{x+9}=\frac{2}{x} x+9x−5​=x2​\newlineAnswer: x= x= x=

Solve for all values of $x$ . $\newline$ $\frac{x-5}{x+9}=\frac{2}{x}$ $\newline$ Answer: $x=$