AI tutor
Full solution
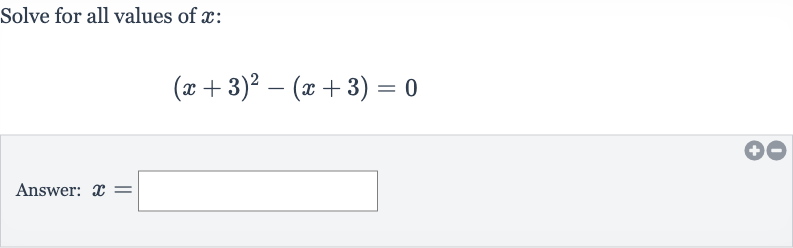
Q. Solve for all values of :Answer:
- Factor out common term: Factor out the common term from the equation.We have the equation . Notice that is a common term in both parts of the equation. We can factor it out to simplify the equation.
- Apply zero-product property: Apply the zero-product property.If the product of two factors is zero, then at least one of the factors must be zero. Therefore, we can set each factor equal to zero and solve for . or
- Solve first equation: Solve the first equation for .Subtract from both sides to isolate .
- Solve second equation: Solve the second equation for .Subtract from both sides to isolate .
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help