AI tutor
Full solution
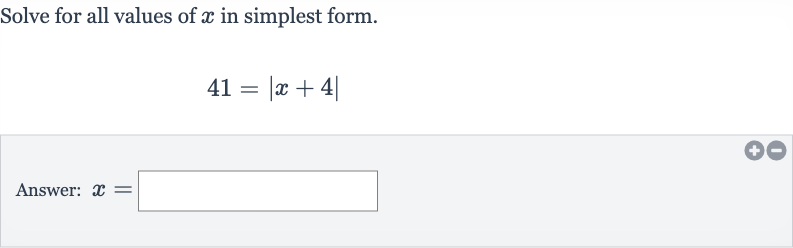
Q. Solve for all values of in simplest form.Answer:
- Understand absolute value equation: Understand the absolute value equation.The absolute value of a number is its distance from zero on the number line, regardless of direction. Therefore, can be either or if is positive or negative, respectively. We need to consider both cases to find all values of .
- Set up two equations: Set up two separate equations to solve.Since the absolute value of is equal to , we have two possible equations:) )
- Solve first equation: Solve the first equation.Starting with , we subtract from both sides to isolate :
- Solve second equation: Solve the second equation.Now, we solve . First, we distribute the negative sign:Next, we add to both sides to isolate :Finally, we multiply both sides by to solve for :
More problems from Multiply numbers ending in zeros
QuestionGet tutor help
QuestionGet tutor help