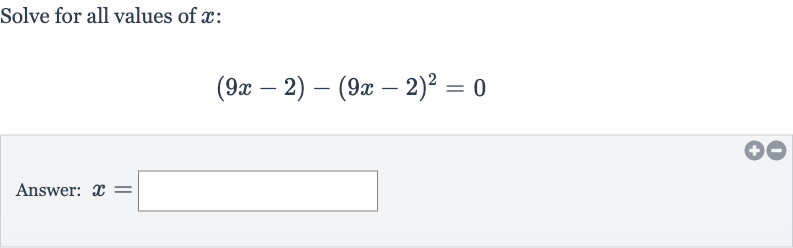AI tutor
Full solution
Q. Solve for all values of :Answer:
- Expand and Simplify: Simplify the equation by expanding the squared term.We have the equation . Let's expand the squared term.
- Distribute Negative Sign: Distribute the negative sign through the squared term.We need to apply the negative sign to each term in the squared expression.
- Combine Like Terms: Combine like terms.Now we combine the like terms on the left side of the equation.
- Factor Out Common Factor: Continue combining like terms.Combine the terms and the constant terms.
- Find Quadratic Factors: Factor out the greatest common factor.We can factor out a from each term.
- Apply Quadratic Formula: Look for factors of the quadratic equation.This is a quadratic equation in the form . We need to find factors or use the quadratic formula to solve for . However, this equation does not factor nicely, so we will use the quadratic formula.
- Simplify and Solve: Apply the quadratic formula.Let's plug in the values , , and into the quadratic formula.
- Simplify and Solve: Apply the quadratic formula.Let's plug in the values , , and into the quadratic formula. Simplify under the square root and solve for x.
- Simplify and Solve: Apply the quadratic formula.Let's plug in the values , , and into the quadratic formula. Simplify under the square root and solve for x. Solve for the two possible values of x. or or
- Simplify and Solve: Apply the quadratic formula.Let's plug in the values , , and into the quadratic formula. Simplify under the square root and solve for x. Solve for the two possible values of x. or or Simplify both fractions. or
More problems from Composition of linear and quadratic functions: find a value
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help