AI tutor
Full solution
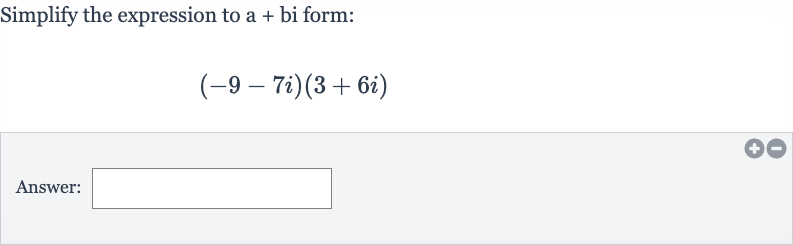
Q. Simplify the expression to a + bi form:Answer:
- Apply Distributive Property: First, we need to apply the distributive property (also known as the FOIL method for binomials) to multiply the two complex numbers.
- Calculate Each Part: Now, we calculate each part of the expression separately. (Remember that )
- Combine Real and Imaginary Parts: Next, we combine the real parts and the imaginary parts and simplify using .
Real part:
Imaginary part:
And for the term with : - Add Real and Imaginary Parts: Now, we add the real part and the simplified term with together, and then combine it with the imaginary part.Real part: Imaginary part: So, the expression in form is .