AI tutor
Full solution
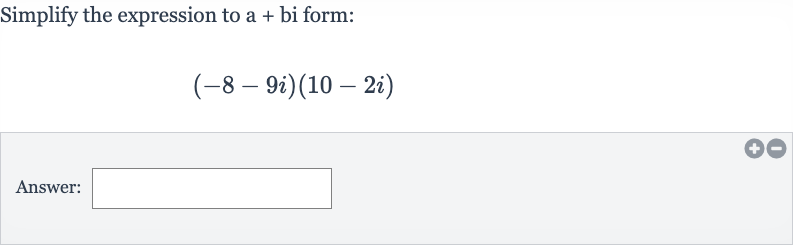
Q. Simplify the expression to a + bi form:Answer:
- Apply Distributive Property: To simplify the expression , we will use the distributive property (also known as the FOIL method for binomials), which involves multiplying each term in the first complex number by each term in the second complex number.
- Multiply Real Parts: First, we multiply the real parts: .
- Multiply Real and Imaginary Parts: Next, we multiply the real part of the first complex number by the imaginary part of the second complex number: .
- Multiply Imaginary Parts: Then, we multiply the imaginary part of the first complex number by the real part of the second complex number: .
- Combine Terms: Finally, we multiply the imaginary parts: . Since , this simplifies to .
- Combine Terms: Finally, we multiply the imaginary parts: . Since , this simplifies to .Now, we combine all the terms: (from the first step) + (from the second step) - (from the third step) - (from the fourth step).
- Combine Terms: Finally, we multiply the imaginary parts: . Since , this simplifies to .Now, we combine all the terms: (from the first step) + (from the second step) - (from the third step) - (from the fourth step).Combining like terms, we get: .