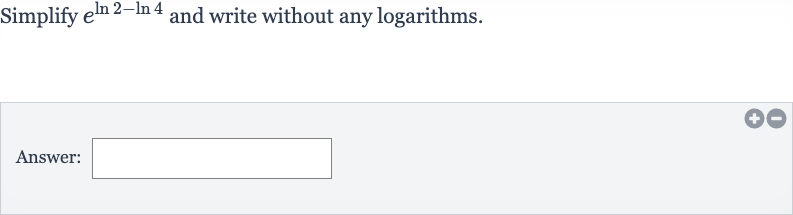
Simplify e^(ln 2-ln 4) and write without any logarithms. Answer:

Question

Simplify  e^(ln 2-ln 4) and write without any logarithms. Answer:

Bytelearn · Accepted Answer

Understand Properties: Understand the properties of logarithms and exponents. The expression e^(ln 2 - ln 4) involves the natural logarithm, ln, and the natural exponential function, e. The natural logarithm ln(x) is the inverse function of the exponential function e^x. Therefore, e^(ln x) = x for any positive number x. Also, the difference of logarithms ln(a) - ln(b) is equivalent to the logarithm of the division of a by b, ln(a/b). We will use these properties to simplify the expression.Combine Logarithms: Apply the logarithm property to combine the logarithms. Using the property that ln(a) - ln(b) = ln(a/b), we can rewrite the exponent as a single logarithm: e^(ln 2 - ln 4) = e^(ln(2/4)).Simplify Fraction: Simplify the fraction inside the logarithm. The fraction 2/4 can be simplified to 1/2, so we have: e^(ln(2/4)) = e^(ln(1/2)).Apply Inverse Property: Apply the inverse property of logarithms and exponents. Using the property that e^(ln x) = x, we can simplify the expression to get the final result: e^(ln(1/2)) = 1/2.

Simplify $e^{\ln 2-\ln 4}$ and write without any logarithms. $\newline$ Answer:

Full solution

More problems from Find the roots of factored polynomials

Related topics

Simplify eln⁡2−ln⁡4 e^{\ln 2-\ln 4} eln2−ln4 and write without any logarithms.\newlineAnswer:

Simplify $e^{\ln 2-\ln 4}$ and write without any logarithms. $\newline$ Answer: