AI tutor
Full solution
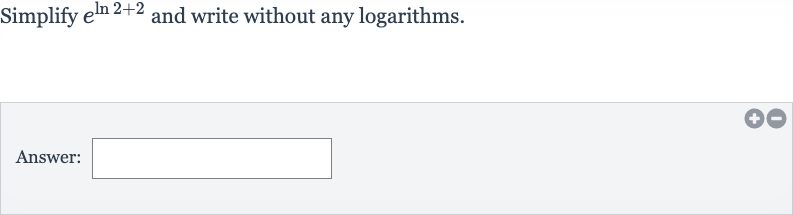
Q. Simplify and write without any logarithms.Answer:
- Break down expression: The expression can be broken down into two parts: and . We know that for any , because the natural logarithm function is the inverse of the exponential function . Therefore, simplifies to .
- Simplify : Now we need to consider the second part of the expression, which is . This part remains as it is because it does not involve a logarithm and is already in its simplest exponential form.
- Combine parts: Combining the two parts together, we have . This is the simplified form of the original expression without any logarithms.