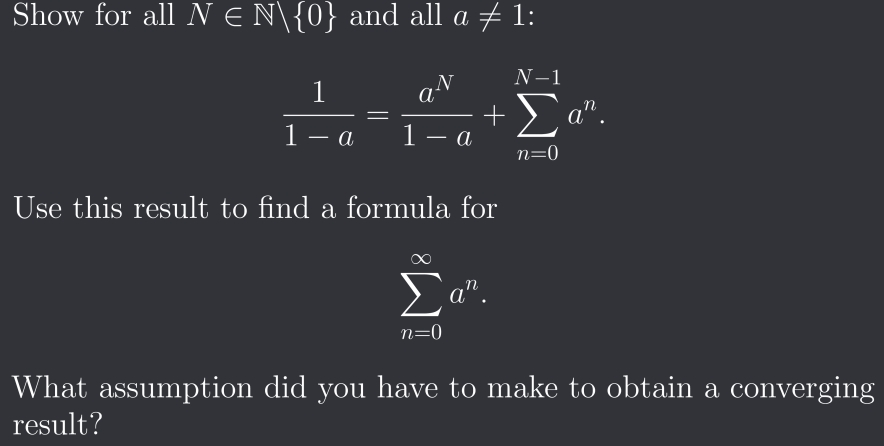Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

$Show for all N inN\\{0} and all a!=1 : (1)/(1-a)=(a^(N))/(1-a)+sum_(n=0)^(N-1)a^(n). Use this result to find a formula for sum_(n=0)^(oo)a^(n). What assumption did you have to make to obtain a converging result?$

Show for all $N \in \mathbb{N}\setminus\{0\}$ and all $a \neq 1$ : $\newline$ $\frac{1}{1-a} = \frac{a^N}{1-a} + \sum_{n=0}^{N-1}a^n$ . $\newline$ Use this result to find a formula for $\newline$ $\sum_{n=0}^{\infty}a^n$ . $\newline$ What assumption did you have to make to obtain a converging result?

View step-by-step help

View step-by-step help

Find instantaneous rates of change

Full solution

Q. Show for all

N \in \mathbb{N}\setminus\{0\}

and all

a \neq 1

:

\newline

\frac{1}{1-a} = \frac{a^N}{1-a} + \sum_{n=0}^{N-1}a^n

.

\newline

Use this result to find a formula for

\newline

\sum_{n=0}^{\infty}a^n

.

\newline

What assumption did you have to make to obtain a converging result?

Evaluate RHS: We are given the equation: $\newline$ $\frac{1}{1-a} = \frac{a^N}{1-a} + \sum_{n=0}^{N-1}a^n$ $\newline$ We need to show that this equation holds for all $N \in \mathbb{N}\setminus\{0\}$ and for all $a \neq 1$ . $\newline$ Let's start by evaluating the right-hand side of the equation.
Finite Geometric Series: First, we consider the finite geometric series $\sum_{n=0}^{N-1}a^n$ . The formula for the sum of a finite geometric series is: $S_N = a^0 + a^1 + a^2 + \ldots + a^{N-1} = \frac{1 - a^N}{1 - a}$ , for $a \neq 1$ .
Substitute into RHS: Now, let's substitute $S_N$ into the right-hand side of the given equation: $\newline$ $\frac{a^N}{1-a} + \sum_{n=0}^{N-1}a^n = \frac{a^N}{1-a} + \frac{1 - a^N}{1 - a}$ .
Simplify RHS: We simplify the right-hand side: $\newline$ (a^N)/(\(1-a) + ( $1$ - a^N) / ( $1$ - a) = (a^N - a^N + $1$ ) / ( $1$ - a) = $1$ / ( $1$ - a)\.
Show Equation Holds: We have shown that: $\newline$ $\frac{1}{1-a} = \frac{a^N}{1-a} + \sum_{n=0}^{N-1}a^n$ $\newline$ This holds for all $N \in \mathbb{N}\setminus\{0\}$ and for all $a \neq 1$ .
Find Infinite Series Formula: Now, we want to find a formula for the infinite series $\sum_{n=0}^{\infty}a^n$ . We assume that $|a| < 1$ for the series to converge.
Limit as $N$ Approaches Infinity: As $N$ approaches infinity, $a^N$ approaches $0$ if $|a| < 1$ . So, the sum of the infinite series is: $\lim_{N\to\infty} S_N = \lim_{N\to\infty} \frac{1 - a^N}{1 - a} = \frac{1}{1 - a}$ .
Convergence Assumption: The assumption we made for the series to converge is that the absolute value of $a$ is less than $1$ , i.e., $|a| < 1$ .

More problems from Find instantaneous rates of change

Question

Consider the curve given by the equation

x y^{2}+5 x y=50

. It can be shown that

\frac{d y}{d x}=\frac{-y(y+5)}{x(2 y+5)} \text {. }

\newline

Write the equation of the vertical line that is tangent to the curve.

Posted 1 month ago

Question

The rate of change

\frac{d P}{d t}

of the number of algae in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2317}{10614} P\left(1-\frac{P}{662}\right)

\newline

t=0

, the number of algae in the tank is

174

and is increasing at a rate of

28

algae per minute. At what value of

P

P(t)

growing the fastest?

\newline

Posted 2 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of bacteria in a tank is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2}{9849} P(598-P)

\newline

t=0

, the number of bacteria in the tank is

196

and is increasing at a rate of

16

bacteria per minute. At what value of

P

does the graph of

P(t)

have an inflection point?

\newline

Posted 2 months ago

Question

The rate of change

\frac{d P}{d t}

of the number of people infected by a disease is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{45}{125404} P(800-P)

\newline

t=0

, the number of people infected by the disease is

214

and is increasing at a rate of

45

people per hour. What is the limiting value for the total number of people infected by the disease as time increases?

\newline

Posted 2 months ago

Question

Which of the following is a correct interpretation of the expression

\newline

-4+13

\newline

1

\newline

(A) The number that is

4

-13

on the number line

\newline

(B) The number that is

4

to the right of

-13

on the number line

\newline

(C) The number that is

13

-4

on the number line

\newline

(D) The number that is

13

to the right of

-4

on the number line

Posted 2 months ago

Question

f

f(x)=x^{3}+2 \sin (3 x-3)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=0.5

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{2}-2 x+3 \cos \left(x^{2}-x\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=-2.5

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{2}+x-2 \sin (2 x)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=3

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{3}+\cos \left(2 x^{2}+5\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=1

. You should round all decimals to

3

\newline

Posted 2 months ago

Question

f

f(x)=x^{3}+3-5 \sin \left(x^{2}\right)

. Use a calculator to write the equation of the line tangent to the graph of

f

x=1

. You should round all decimals to

3

\newline

Posted 2 months ago