Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

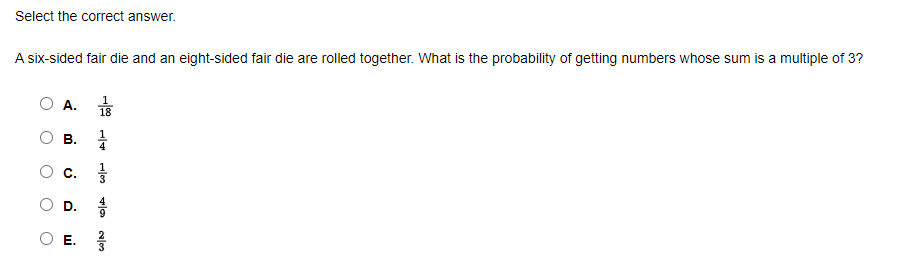
Select the correct answer.
A six-sided fair die and an eight-sided fair die are rolled together. What is the probability of getting numbers whose sum is a multiple of 3 ?
A.
(1)/(18)
B.
(1)/(4)
c.
(1)/(3)
D.
(4)/(9)
E.
(2)/(3)

Select the correct answer. $\newline$ A six-sided fair die and an eight-sided fair die are rolled together. What is the probability of getting numbers whose sum is a multiple of $3$ ? $\newline$ A. $\frac{1}{18}$ $\newline$ B. $\frac{1}{4}$ $\newline$ c. $\frac{1}{3}$ $\newline$ D. $\frac{4}{9}$ $\newline$ E. $\frac{2}{3}$

View step-by-step help

View step-by-step help

Theoretical probability

Full solution

Q. Select the correct answer.

\newline

A six-sided fair die and an eight-sided fair die are rolled together. What is the probability of getting numbers whose sum is a multiple of

3

?

\newline

A.

\frac{1}{18}

\newline

B.

\frac{1}{4}

\newline

c.

\frac{1}{3}

\newline

D.

\frac{4}{9}

\newline

E.

\frac{2}{3}

Calculate Total Outcomes: First, let's determine the total number of possible outcomes when rolling two dice, one with $6$ sides and one with $8$ sides. The total number of outcomes is the product of the number of sides on each die. $\newline$ Total outcomes = $6$ (from the six-sided die) $\times$ $8$ (from the eight-sided die) = $48$ .
Find Favorable Outcomes: Next, we need to find the number of favorable outcomes, which are the pairs of numbers that add up to a multiple of $3$ . We can list these pairs or use a systematic approach to count them.
List Pairs Summing to $3$ : Let's list the pairs that sum to a multiple of $3$ : $(1,2)$ , $(1,5)$ , $(1,8)$ , $(2,1)$ , $(2,4)$ , $(2,7)$ , $(3,3)$ , $(3,6)$ , $(4,2)$ , $(1,2)$ $0$ , $(1,2)$ $1$ , $(1,2)$ $2$ , $(1,2)$ $3$ , $(1,2)$ $4$ , $(1,2)$ $5$ , $(1,2)$ $6$ .
Count Favorable Outcomes: Counting the pairs listed, we have a total of $16$ favorable outcomes.
Calculate Probability: Now, we can calculate the probability of getting a sum that is a multiple of $3$ by dividing the number of favorable outcomes by the total number of possible outcomes. $\text{Probability} = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}} = \frac{16}{48}$ .
Simplify Fraction: Simplify the fraction $\frac{16}{48}$ to its lowest terms. $\newline$ $\frac{16}{48}$ can be simplified by dividing both the numerator and the denominator by $16$ . $\newline$ $\frac{16}{48} = \frac{1}{3}$ .

More problems from Theoretical probability

Question

6

-sided die two times. What is the probability of rolling a number greater than \(3\) and then rolling a number less than \(4\)? Write your answer as a percentage. ____ `%`

Posted 1 month ago

Question

9

college students running for student government class president. The candidates include

7

education majors.

\newline

6

of the candidates are randomly chosen to give the first

6

speeches, what is the probability that all of them are education majors?

\newline

Write your answer as a decimal rounded to four decimal places.

Posted 2 months ago

Question

In an experiment, the probability that event

A

\frac{2}{7}

, the probability that event

B

\frac{7}{9}

, and the probability that events

A

B

\frac{1}{9}

\newline

A

B

independent events?

\newline

\newline

\text{yes}

\newline

\text{no}

Posted 2 months ago

Question

At a science museum, visitors can compete to see who has a faster reaction time. Competitors watch a red screen, and the moment they see it turn from red to green, they push a button. The machine records their reaction times and also asks competitors to report their gender.

\newline

The probability that a competitor reacted in over

0.7

0.6

, the probability that a competitor was female is

0.4

, and the probability that a competitor reacted in over

0.7

seconds and was female is

0.3

\newline

What is the probability that a randomly chosen competitor reacted in over

0.7

seconds or was female?

\newline

Write your answer as a whole number, decimal, or simplified fraction.

\newline

Posted 2 months ago

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 2 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 2 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 2 months ago