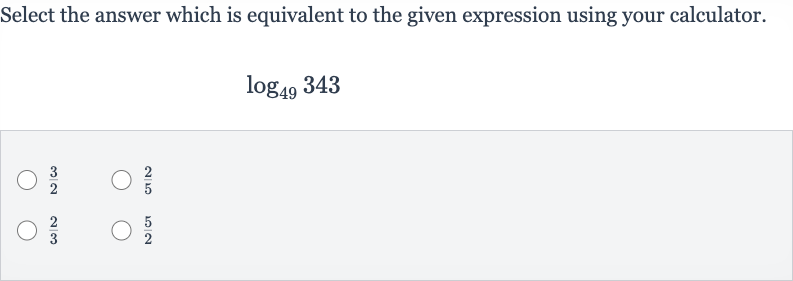Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Select the answer which is equivalent to the given expression using your calculator.

log_(49)343

(3)/(2)

(2)/(5)

(2)/(3)

(5)/(2)

Select the answer which is equivalent to the given expression using your calculator. $\newline$ $\log _{49} 343$ $\newline$ $\frac{3}{2}$ $\newline$ $\frac{2}{5}$ $\newline$ $\frac{2}{3}$ $\newline$ $\frac{5}{2}$

View step-by-step help

View step-by-step help

Quotient property of logarithms

Full solution

Q. Select the answer which is equivalent to the given expression using your calculator.

\newline

\log _{49} 343

\newline

\frac{3}{2}

\newline

\frac{2}{5}

\newline

\frac{2}{3}

\newline

\frac{5}{2}

Recognize Relationship: We need to evaluate the expression $\log_{49}343$ . To do this, we can use the change of base formula for logarithms, which states that $\log_{a}b$ can be written as $\frac{\log(b)}{\log(a)}$ , where $\log$ denotes the common logarithm. However, since we are dealing with specific numbers, we can look for a relationship between the base and the number.
Rewrite Using Properties: We recognize that $49$ is a power of $7$ , specifically $7^2$ , and $343$ is also a power of $7$ , specifically $7^3$ . This can be written as $49 = 7^2$ and $343 = 7^3$ .
Apply Power Rule: Using the property of logarithms that $\log_{a} a^{k} = k$ , we can rewrite $\log_{49}343$ as $\log_{7^2}(7^3)$ . According to the power rule of logarithms, which states that $\log_{a} b^{k} = k \cdot \log_{a} b$ , we can simplify this expression.
Apply Power Rule: Using the property of logarithms that $\log_{a} a^{k} = k$ , we can rewrite $\log_{(49)}343$ as $\log_{(7^2)}(7^3)$ . According to the power rule of logarithms, which states that $\log_{a} b^{k} = k \cdot \log_{a} b$ , we can simplify this expression.Applying the power rule, we get $\log_{(7^2)}(7^3) = \frac{3}{2}$ , because we are taking the logarithm of a cube ( $343$ is $7$ cubed) with respect to the square of the same base ( $49$ is $7$ squared).

More problems from Quotient property of logarithms

Question

x

\newline

5^x=1

\newline

\newline

Write your answer in simplest form.

Posted 5 months ago

Question

Steven opened a savings account and deposited

\$100.00

as principal. The account earns

9\%

interest, compounded annually. What is the balance after

5

\newline

Use the formula

A = P(1 + \frac{r}{n})^{nt}

A

is the balance (final amount),

P

is the principal (starting amount),

r

is the interest rate expressed as a decimal,

n

is the number of times per year that the interest is compounded, and

t

is the time in years.

\newline

Round your answer to the nearest cent.

Posted 4 months ago

Question

Use the following function rule to find

f(1)

\newline

f(x) = 12(7)^x + 8

Posted 5 months ago

Question

The town of Valley View conducted a census this year, which showed that it has a population of

1,800

people. Based on the census data, it is estimated that the population of Valley View will grow by

12\%

\newline

Write an exponential equation in the form

y = a(b)^x

that can model the town population,

y

x

decades after this census was taken.

\newline

Use whole numbers, decimals, or simplified fractions for the values of

a

b

\newline

y =

Posted 8 months ago

Question

x

\newline

7 = 9^x

\newline

Round your answer to the nearest thousandth.

Posted 4 months ago

Question

Solve. Round your answer to the nearest thousandth.

\newline

7 = e^x

\newline

x =

Posted 7 months ago

Question

Solve. Simplify your answer.

\newline

\log u = 1

\newline

u =

Posted 9 months ago

Question

Solve. Simplify your answer.

\newline

7\log x = 7

\newline

x =

Posted 7 months ago

Question

g(t) = 3^t

change over the interval from

t = 3

t = 4

\newline

\newline

g(t)

3

\newline

g(t)

3

\newline

g(t)

3\%

\newline

g(t)

200\%

Posted 4 months ago

Question

f(x)

6

over every unit interval in

x

f(0) = 0

\newline

Which could be a function rule for

f(x)

\newline

\newline

f(x) = 6x

\newline

f(x) = 6^x

\newline

f(x) = \frac{1}{6^x}

\newline

f(x) = \frac{x}{6}

Posted 4 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant