Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Score: 4/5
Penalty: none
Question
Watch Video
Show Examples
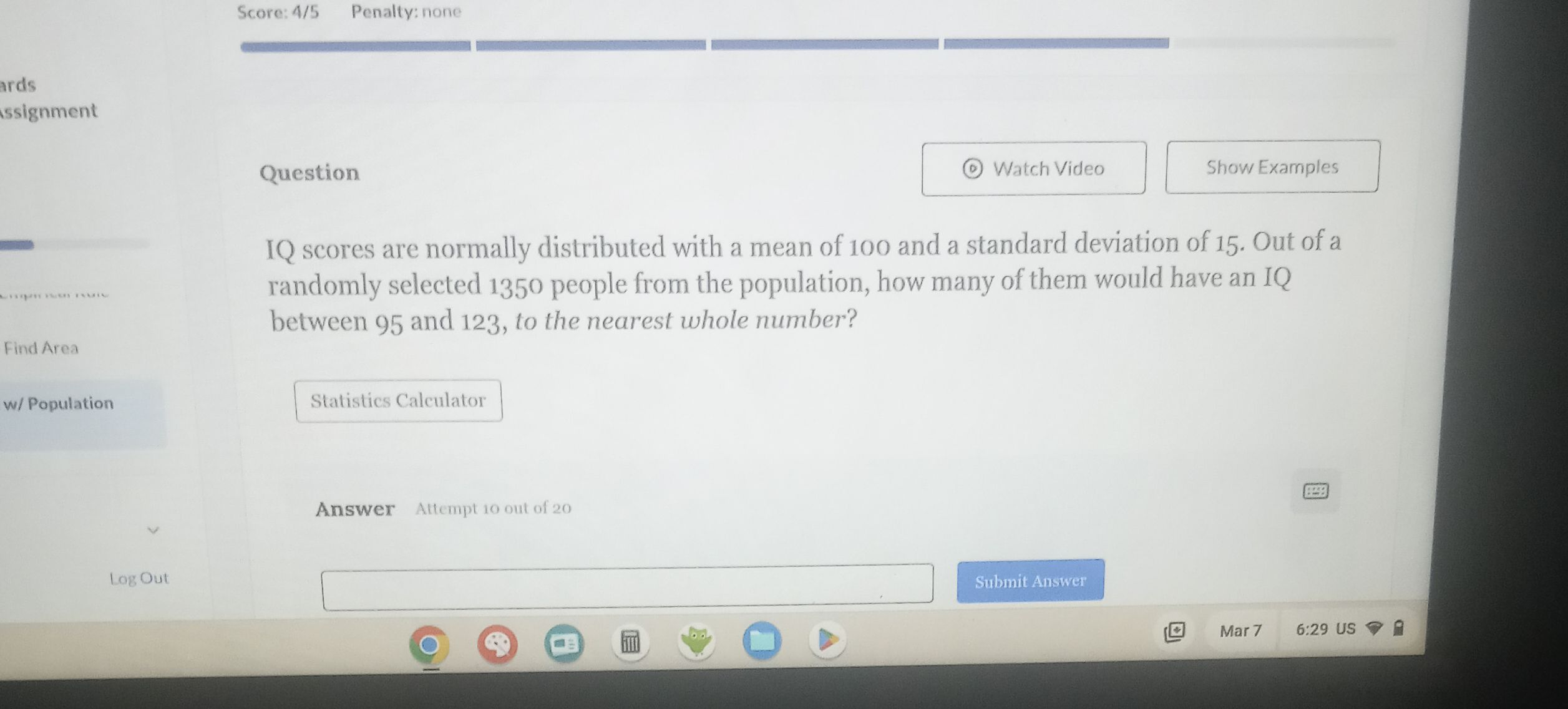
IQ scores are normally distributed with a mean of 100 and a standard deviation of 15 . Out of a randomly selected 1350 people from the population, how many of them would have an IQ between 95 and 123 , to the nearest whole number?
Find Area
w/ Population
Statistics Calculator
Answer Altempt 10 out of 20
Log Out
Submit Answer
Mar 7
6:29 US
g

Score: $4$ / $5$ $\newline$ Penalty: none $\newline$ Question $\newline$ Watch Video $\newline$ Show Examples $\newline$ IQ scores are normally distributed with a mean of $100$ and a standard deviation of $15$ . Out of a randomly selected $1350$ people from the population, how many of them would have an IQ between $95$ and $123$ , to the nearest whole number? $\newline$ Find Area $\newline$ w/ Population $\newline$ Statistics Calculator $\newline$ Answer Altempt $10$ out of $20$ $\newline$ Log Out $\newline$ Submit Answer $\newline$ Mar $7$ $\newline$ $6$ : $29$ US $\newline$ g

View step-by-step help

View step-by-step help

Scale drawings: word problems

Full solution

Q. Score:

4

/

5

\newline

Penalty: none

\newline

Question

\newline

Watch Video

\newline

Show Examples

\newline

IQ scores are normally distributed with a mean of

100

and a standard deviation of

15

. Out of a randomly selected

1350

people from the population, how many of them would have an IQ between

95

and

123

, to the nearest whole number?

\newline

Find Area

\newline

w/ Population

\newline

Statistics Calculator

\newline

Answer Altempt

10

out of

20

\newline

Log Out

\newline

Submit Answer

\newline

Mar

7

\newline

6

:

29

US

\newline

g

Identify Mean and Standard Deviation: Identify the mean and standard deviation of the IQ scores. $\newline$ Mean ( $\mu$ ) = $100$ $\newline$ Standard deviation ( $\sigma$ ) = $15$
Calculate Z-Scores: Calculate the z-scores for the IQ scores of $95$ and $123$ . The z-score formula is $z = \frac{X - \mu}{\sigma}$ , where $X$ is the value from the data set. For IQ = $95$ : $z = \frac{95 - 100}{15} = \frac{-5}{15} = -\frac{1}{3} \approx -0.33$ For IQ = $123$ : $z = \frac{123 - 100}{15} = \frac{23}{15} \approx 1.53$
Find Area Under the Curve: Use the standard normal distribution table or a calculator to find the area under the curve between the $z$ -scores of $-0.33$ and $1.53$ . The area under the curve from the mean to $z = -0.33$ is approximately $0.3707$ . The area under the curve from the mean to $z = 1.53$ is approximately $0.9370$ .
Calculate Area Between Z-Scores: Calculate the area between the two z-scores by subtracting the area from the mean to $z = -0.33$ from the area from the mean to $z = 1.53$ . $\newline$ Area between $z = -0.33$ and $z = 1.53$ = $0.9370 - 0.3707 = 0.5663$
Find Number of People: Multiply the area by the total number of people to find the number of people with an IQ between $95$ and $123$ . $\newline$ Number of people $=$ Total population $\times$ Area between $z$ -scores $\newline$ Number of people $= 1350 \times 0.5663 \approx 764.805$
Round to Nearest Whole Number: Round the result to the nearest whole number, as we cannot have a fraction of a person. $\newline$ Number of people $\approx 765$

More problems from Scale drawings: word problems

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 2 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 2 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 2 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 2 months ago

Question

\newline

500

=

Posted 3 months ago

Question

\newline

2,000

=

Posted 3 months ago

Question

\newline

750

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago

Question

\newline

1,500

=

Posted 3 months ago

Question

The formula for the time it takes to travel a distance of

d

at an average speed

v

\frac{d}{v}

100

-meter dash at a speed of about

7.5

meters per second. What calculation will give us the estimated duration of Tessa's dash in seconds? Choose

1

\newline

\frac{7.5}{100}

\newline

\frac{100}{7.5}

\newline

\frac{7.5}{100 \times 60}

\newline

\frac{100 \times 60}{7.5}

Posted 4 months ago