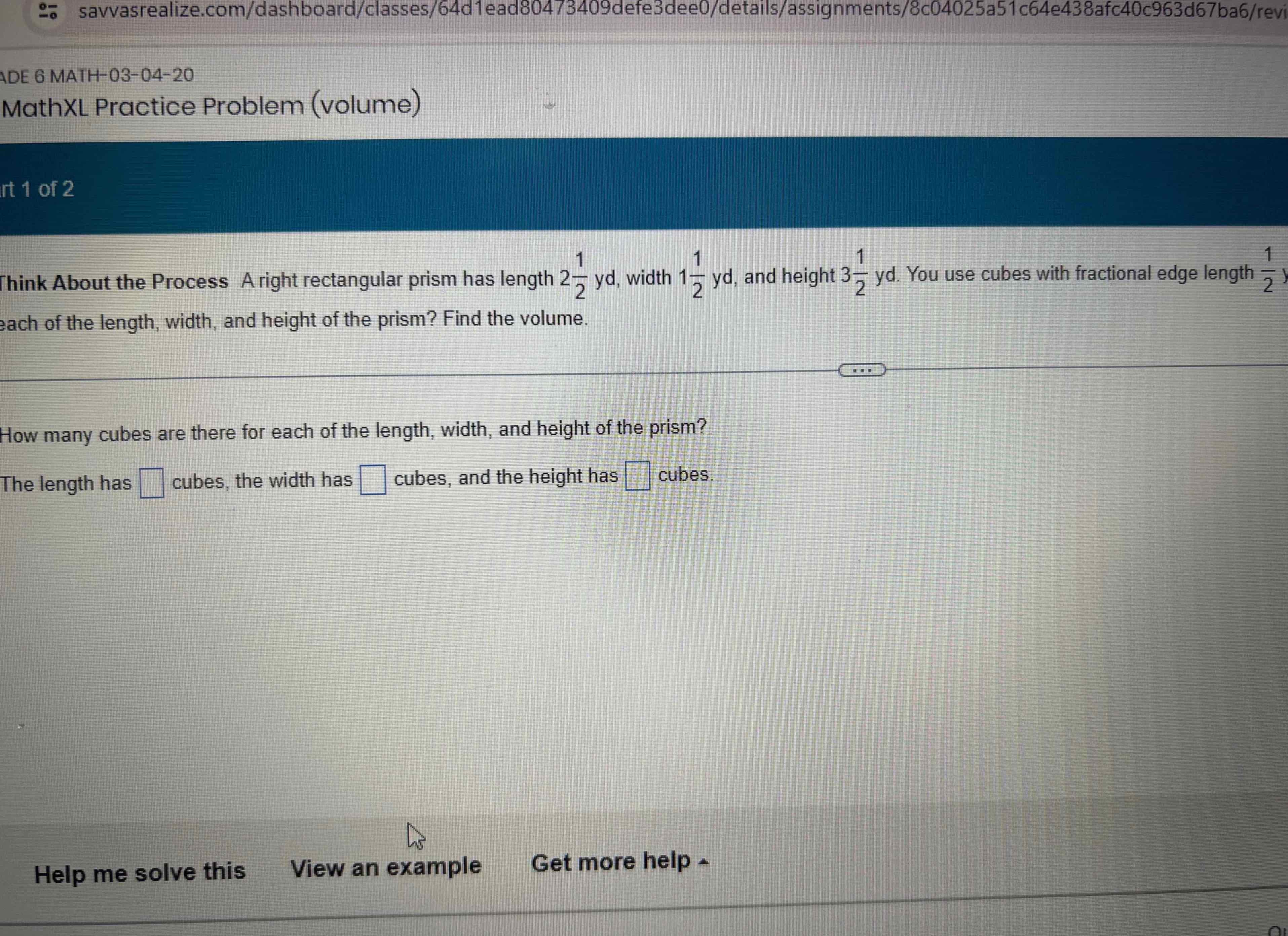
A right rectangular prism has length 2(1)/(2) yd, width 1(1)/(2)yd, and height 3(1)/(2) yd. You use cubes with fractional edge length (1)/(2) ) each of the length, width, and height of the prism? Find the volume. How many cubes are there for each of the length, width, and height of the prism? The length has ◻ cubes, the width has ◻ cubes, and the height has ◻ cubes.

Question

A right rectangular prism has length  2(1)/(2) yd, width  1(1)/(2)yd, and height  3(1)/(2) yd. You use cubes with fractional edge length  (1)/(2) ) each of the length, width, and height of the prism? Find the volume. How many cubes are there for each of the length, width, and height of the prism? The length has  ◻ cubes, the width has  ◻ cubes, and the height has  ◻ cubes.

Bytelearn · Accepted Answer

Calculate length cubes:  Calculate the number of cubes along the length of the prism. Length of prism = 2(1)/(2) yd, Cube edge length = (1)/(2) yd. Number of cubes = Length of prism / Cube edge length = 2(1)/(2) / (1)/(2) = 5 cubes. Calculate width cubes:  Calculate the number of cubes along the width of the prism. Width of prism = 1(1)/(2) yd, Cube edge length = (1)/(2) yd. Number of cubes = Width of prism / Cube edge length = 1(1)/(2) / (1)/(2) = 3 cubes. Calculate height cubes:  Calculate the number of cubes along the height of the prism. Height of prism = 3(1)/(2) yd, Cube edge length = (1)/(2) yd. Number of cubes = Height of prism / Cube edge length = 3(1)/(2) / (1)/(2) = 7 cubes.

Full solution

More problems from One-step inequalities: word problems

Related topics