AI tutor
Full solution
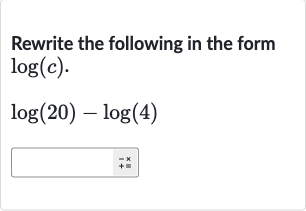
Q. Rewrite the following in the form .
- Identify Property: Identify the property of logarithm used to rewrite . The expression involves the difference of two logarithms with the same base. The quotient property of logarithms states that the difference of two logarithms is the logarithm of the quotient of their arguments.
- Apply Quotient Property: Apply the quotient property to combine - into a single logarithm.Using the quotient property, we can write the difference of the two logarithms as the logarithm of the quotient of their arguments:
- Calculate Quotient: Calculate the quotient inside the logarithm.Calculate the value of divided by :
- Write Final Expression: Write the final expression using the result from Step .Since equals , we can write the expression as:
More problems from Evaluate logarithms using properties
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help