Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Rewrite the expression in the form b^(n). (b^(2))^((3)/(7))=◻

Rewrite the expression in the form bn b^{n} .\newline(b2)37=□ \left(b^{2}\right)^{\frac{3}{7}}=\square

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate exponential functionsright chevron icon

Full solution

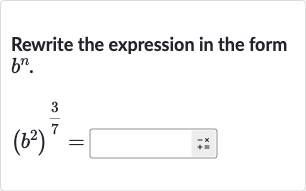
Q. Rewrite the expression in the form bn b^{n} .\newline(b2)37=□ \left(b^{2}\right)^{\frac{3}{7}}=\square
  1. Apply power of power rule: Apply the power of a power rule.\newlineThe power of a power rule states that (am)n=am∗n(a^m)^n = a^{m*n}. We will apply this rule to the given expression (b2)(3)/(7)(b^{2})^{(3)/(7)}.
  2. Multiply exponents: Multiply the exponents.\newlineUsing the power of a power rule, we multiply the exponents 22 and 37\frac{3}{7} together.\newlineb2×(37)=b67b^{2\times\left(\frac{3}{7}\right)} = b^{\frac{6}{7}}
  3. Simplify expression: Simplify the expression.\newlineThe expression b67b^{\frac{6}{7}} is already in the simplest form, so no further simplification is needed.

More problems from Evaluate exponential functions

Question
Solve for xx.\newline5x=15^x=1\newline\newlineWrite your answer in simplest form.
Get tutor helpright-arrow

Posted 5 months ago

Question
Steven opened a savings account and deposited $100.00\$100.00 as principal. The account earns 9%9\% interest, compounded annually. What is the balance after 55 years?\newlineUse the formula A=P(1+rn)ntA = P(1 + \frac{r}{n})^{nt}, where AA is the balance (final amount), PP is the principal (starting amount), rr is the interest rate expressed as a decimal, nn is the number of times per year that the interest is compounded, and tt is the time in years.\newlineRound your answer to the nearest cent.
Get tutor helpright-arrow

Posted 4 months ago

Question
Use the following function rule to find f(1) f(1) .\newlinef(x)=12(7)x+8 f(x) = 12(7)^x + 8
Get tutor helpright-arrow

Posted 5 months ago

Question
The town of Valley View conducted a census this year, which showed that it has a population of 1,8001,800 people. Based on the census data, it is estimated that the population of Valley View will grow by 12%12\% each decade.\newlineWrite an exponential equation in the form y=a(b)xy = a(b)^x that can model the town population, yy, xx decades after this census was taken.\newlineUse whole numbers, decimals, or simplified fractions for the values of aa and bb.\newliney=y = ______
Get tutor helpright-arrow

Posted 8 months ago

Question
Solve for xx. \newline7=9x7 = 9^x\newlineRound your answer to the nearest thousandth.
Get tutor helpright-arrow

Posted 4 months ago

Question
Solve. Round your answer to the nearest thousandth.\newline7=ex7 = e^x\newlinex=x = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
Solve. Simplify your answer.\newlinelog⁡u=1\log u = 1\newlineu=u = ____
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve. Simplify your answer.\newline7log⁡x=77\log x = 7\newlinex=x = ____
Get tutor helpright-arrow

Posted 7 months ago

Question
How does g(t)=3t g(t) = 3^t change over the interval from t=3 t = 3 to t=4 t = 4 ?\newlineChoices:\newline(A) g(t) g(t) decreases by 3 3 \newline(B) g(t) g(t) increases by 3 3 \newline(C) g(t) g(t) decreases by 3% 3\%\newline(D) g(t) g(t) increases by 200%200\%
Get tutor helpright-arrow

Posted 4 months ago

Question
A function f(x) f(x) increases by 6 6 over every unit interval in x x and f(0)=0 f(0) = 0 .\newlineWhich could be a function rule for f(x) f(x) ?\newlineChoices:\newline(A) f(x)=6xf(x) = 6x\newline(B) f(x)=6xf(x) = 6^x\newline(C) f(x)=16xf(x) = \frac{1}{6^x}\newline(D) f(x)=x6f(x) = \frac{x}{6}
Get tutor helpright-arrow

Posted 4 months ago

View all (200)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant