Full solution
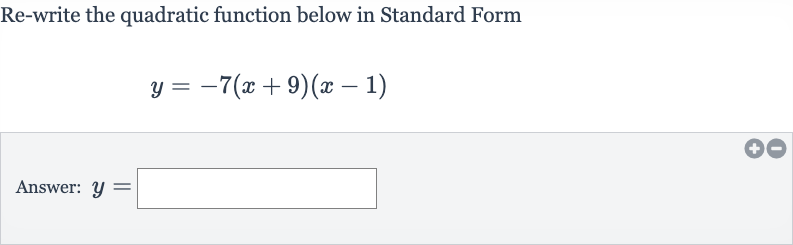
Q. Re-write the quadratic function below in Standard FormAnswer:
- Expand Quadratic Function: Expand the quadratic function using the distributive property (also known as FOIL - First, Outer, Inner, Last).We need to multiply each term in the first binomial by each term in the second binomial.
- Perform Multiplication: Perform the multiplication for each pair of terms.
- Combine Like Terms: Combine like terms inside the brackets.y = y =
- Distribute Coefficients: Distribute the across each term inside the brackets.
- Write in Standard Form: Write the final expression in standard form, which is .This is the standard form of the quadratic function.