Full solution
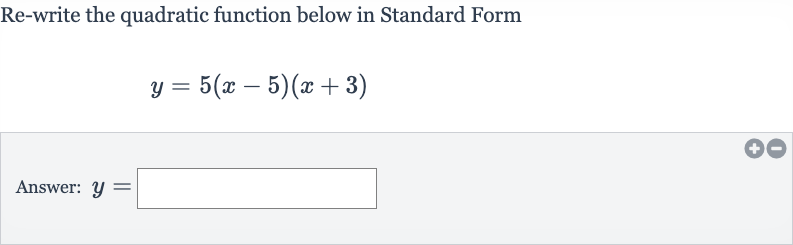
Q. Re-write the quadratic function below in Standard FormAnswer:
- Expand Quadratic Function: Expand the quadratic function using the distributive property (also known as the FOIL method for binomials).We need to multiply the two binomials and together.
- Simplify Expression: Continue simplifying the expression by combining like terms.
- Distribute Coefficients: Distribute the across each term inside the brackets.
- Write in Standard Form: Write the final expression in standard form, which is . The standard form of the quadratic function is: