Full solution
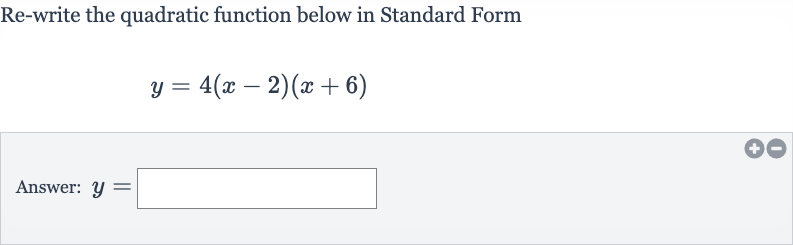
Q. Re-write the quadratic function below in Standard FormAnswer:
- Expand Quadratic Function: Expand the quadratic function using the distributive property (FOIL method). We need to multiply the two binomials and together and then multiply the result by .
- Multiply Binomials: Multiply the terms in the binomials.
- Multiply by : Multiply the result by .