Full solution
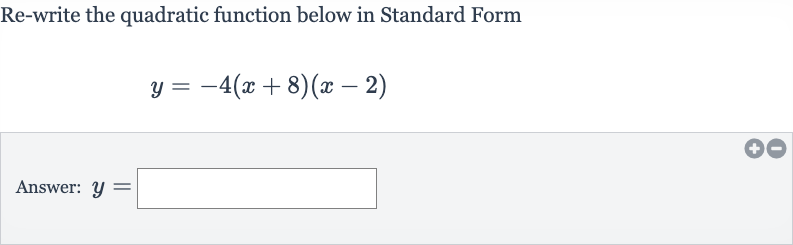
Q. Re-write the quadratic function below in Standard FormAnswer:
- Expand Quadratic Function: Expand the quadratic function using the distributive property (also known as the FOIL method for binomials).We need to multiply each term in the first binomial by each term in the second binomial.
- Perform Multiplication: Perform the multiplication for each pair of terms.y = Combine like terms inside the brackets.y =
- Combine Like Terms: Distribute the across each term inside the brackets.
- Distribute : Write the quadratic function in standard form.The standard form of a quadratic function is .Therefore, the standard form of the given quadratic function is: