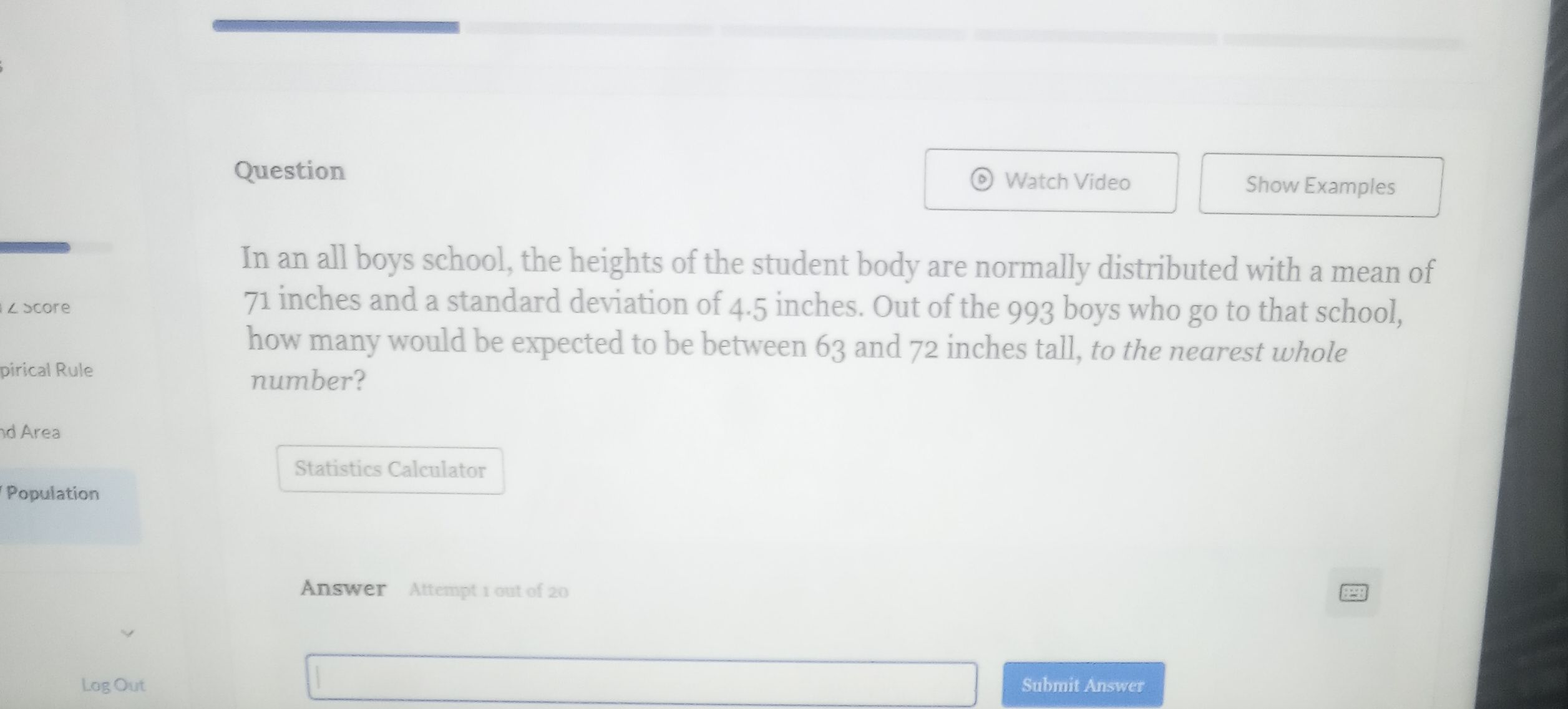
In an all boys school, the heights of the student body are normally distributed with a mean of 71 inches and a standard deviation of 4.5 inches. Out of the 993 boys who go to that school, how many would be expected to be between 63 and 72 inches tall, to the nearest whole number?

Question

Bytelearn · Accepted Answer

Identify Parameters: Identify the parameters of the normal distribution. The mean (μ) is 71 inches, and the standard deviation (σ) is 4.5 inches.Convert Heights to Z-scores: Convert the given heights into z-scores. To find the z-score for 63 inches, we use the formula: z = (X - μ) / σ, where X is the height. For 63 inches: z = (63 - 71) / 4.5 = -8 / 4.5 ≈ -1.78 For 72 inches: z = (72 - 71) / 4.5 = 1 / 4.5 ≈ 0.22Use Normal Distribution Table: Use the standard normal distribution table to find the probabilities corresponding to the z-scores. For z = -1.78, the table gives us a probability of approximately 0.0375. For z = 0.22, the table gives us a probability of approximately 0.5871.Calculate Probability Range: Calculate the probability of a student being between 63 and 72 inches tall. To find this probability, we subtract the probability of z = -1.78 from the probability of z = 0.22. Probability (63 < X < 72) = P(z < 0.22) - P(z < -1.78) ≈ 0.5871 - 0.0375 = 0.5496Calculate Expected Number: Calculate the expected number of boys within the height range. To find the expected number, we multiply the total number of boys by the probability calculated in the previous step. Number of boys = Total number of boys * Probability (63 < X < 72) Number of boys ≈ 993 * 0.5496 ≈ 545.5Round Expected Number: Round the expected number to the nearest whole number. The expected number of boys between 63 and 72 inches tall is approximately 546 when rounded to the nearest whole number.

In an all boys school, the heights of the student body are normally distributed with a mean of $71$ inches and a standard deviation of $4$ . $5$ inches. Out of the $993$ boys who go to that school, how many would be expected to be between $63$ and $72$ inches tall, to the nearest whole number?

Full solution

More problems from Find probabilities using the binomial distribution

Related topics