Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Which of the following functions are continuous for all real numbers?

g(x)=ln(x)

f(x)=(1)/(x)
Choose 1 answer:
(A)
g only
(B)
f only
(C) Both
g and
f
(D) Neither
g nor
f

Which of the following functions are continuous for all real numbers? $\newline$ $g(x)=\ln (x)$ $\newline$ $f(x)=\frac{1}{x}$ $\newline$ Choose $1$ answer: $\newline$ (A) $g$ only $\newline$ (B) $f$ only $\newline$ (C) Both $g$ and $f$ $\newline$ D Neither $g$ nor $f$

View step-by-step help

View step-by-step help

Identify discrete and continuous random variables

Full solution

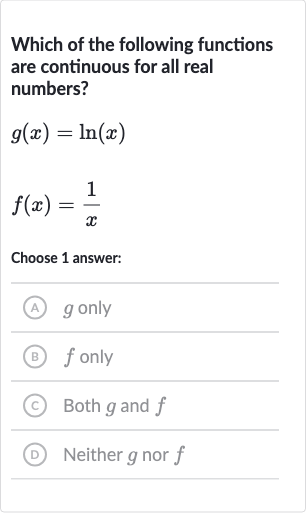
Q. Which of the following functions are continuous for all real numbers?

\newline

g(x)=\ln (x)

\newline

f(x)=\frac{1}{x}

\newline

Choose

1

answer:

\newline

(A)

g

only

\newline

(B)

f

only

\newline

(C) Both

g

and

f

\newline

D Neither

g

nor

f

Determine Continuity: We need to determine the continuity of the functions $g(x) = \ln(x)$ and $f(x) = \frac{1}{x}$ for all real numbers.
Consider $g(x) = \ln(x)$ : Let's first consider $g(x) = \ln(x)$ . The natural logarithm function $\ln(x)$ is defined only for $x > 0$ . Therefore, it is not defined for $x \leq 0$ , which means it is not continuous for all real numbers.
Consider $f(x) = \frac{1}{x}$ : Now let's consider $f(x) = \frac{1}{x}$ . The function $\frac{1}{x}$ is defined for all real numbers except $x = 0$ , where it has a vertical asymptote. Therefore, it is not continuous at $x = 0$ .
Neither g nor f: Since neither $g(x) = \ln(x)$ nor $f(x) = \frac{1}{x}$ is continuous for all real numbers, the correct answer is (D) Neither $g$ nor $f$ .

More problems from Identify discrete and continuous random variables

Question

A restaurant server claims that \(28\)% of the time he leaves candy with the bill, the customer tips well.

\newline

If the server's claim is true, and one day he leaves candy with \(4\) customers' bills, what is the probability that exactly \(3\) of those customers will tip well?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

Posted 1 month ago

Question

There is a spinner with `50` equally likely sections, numbered from `1` to `50`. You have the opportunity to spin it. If the number is odd, you win $`11`. If the number is even, you win nothing. If you play the game, what is the expected payoff?\(\$\)_____

Posted 2 months ago

Question

There are two different raffles you can enter.

\newline

In raffle A, one ticket will win a `$720` prize, and the other tickets will win nothing. There are

1,000

in the raffle, each costing `$11`.

\newline

Raffle B is for a `$370` prize. Out of

125

tickets, each costing `$5`, one ticket will win the prize, and the other tickets will win nothing.

\newline

Which raffle is a better deal?

\newline

\newline

\text{[A]Raffle A}

\newline

\text{[B]Raffle B}

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

49

and standard deviation

25

\newline

What is the probability that

X

24

74

?

\newline

0.68-0.95-0.997

rule and write your answer as a decimal. Round to the nearest thousandth if necessary.

\newline

Posted 2 months ago

Question

X

is a normally distributed random variable with mean

65

and standard deviation

8

\newline

What is the probability that

X

62

68

?

\newline

Write your answer as a decimal rounded to the nearest thousandth.

\newline

Posted 2 months ago

Question

Complete the statement. Round your answer to the nearest thousandth.

\newline

In a population that is normally distributed with mean

43

and standard deviation

3

30\%

of the values are those less than ______.

Posted 2 months ago

Question

Y

is the number of desserts available in a randomly chosen restaurant.

\newline

Is the random variable

Y

discrete or continuous?

\newline

\newline

\text{[A]discrete}

\newline

\text{[B]continuous}

Posted 2 months ago

Question

Which of the following functions are continuous at

x=-1

\newline

g(x)=\sin (x+1)

\newline

f(x)=\frac{1}{x-1}

\newline

1

\newline

g

\newline

f

\newline

g

f

\newline

g

f

Posted 2 months ago

Question

g

be a continuous function on the closed interval

[-1,4]

g(-1)=-4

g(4)=1

\newline

Which of the following is guaranteed by the Intermediate Value Theorem?

\newline

1

\newline

g(c)=-3

for at least one

c

-1

4

\newline

g(c)=3

for at least one

c

-4

1

\newline

g(c)=-3

for at least one

c

-4

1

\newline

g(c)=3

for at least one

c

-1

4

Posted 1 month ago

Question

45

Posted 12 hours ago