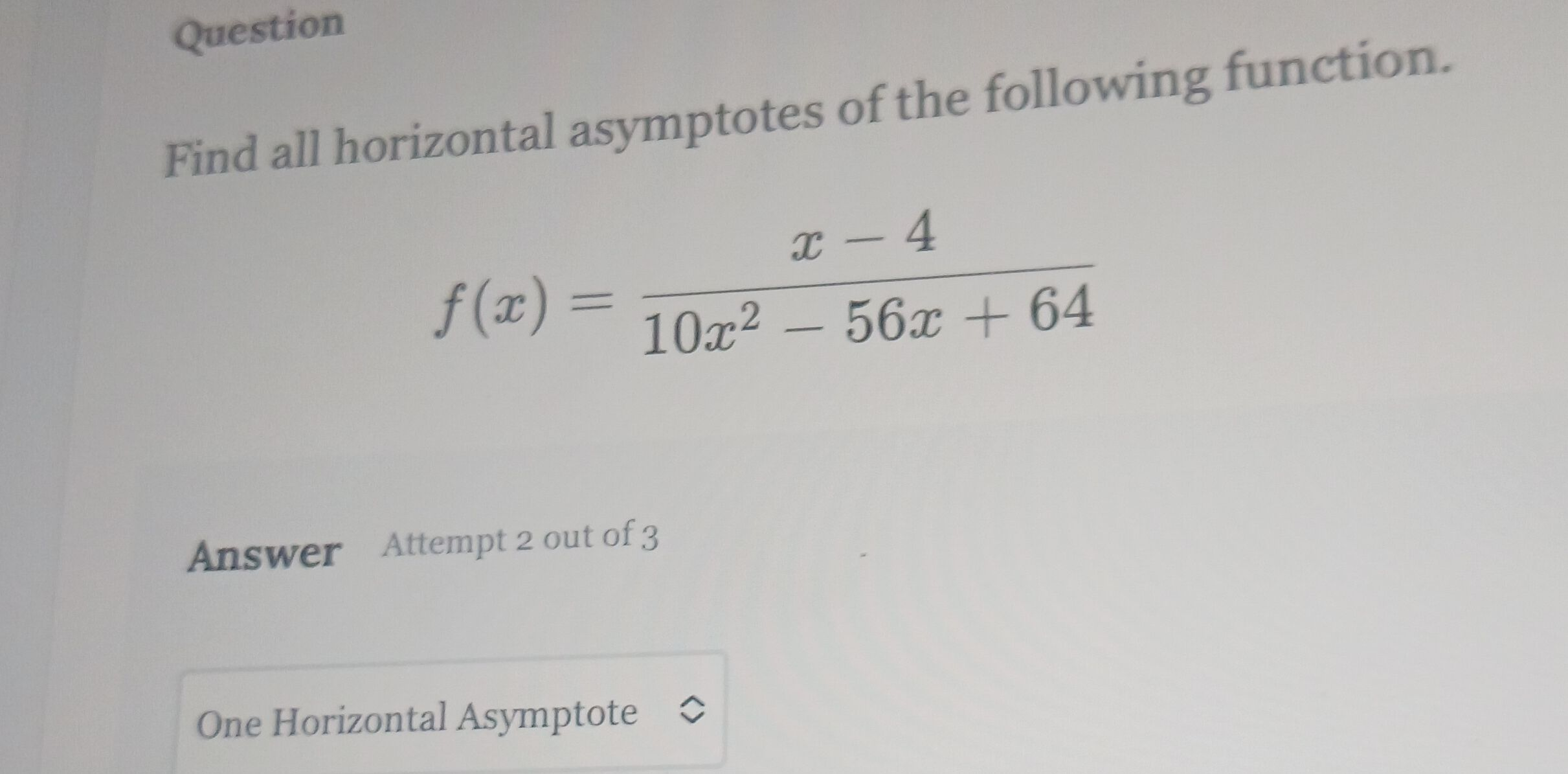Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Question
Find all horizontal asymptotes of the following function.

f(x)=(x-4)/(10x^(2)-56 x+64)

Question $\newline$ Find all horizontal asymptotes of the following function. $\newline$ $f(x)=\frac{x-4}{10 x^{2}-56 x+64}$ $\newline$

View step-by-step help

View step-by-step help

Find the roots of factored polynomials

Full solution

Q. Question

\newline

Find all horizontal asymptotes of the following function.

\newline

f(x)=\frac{x-4}{10 x^{2}-56 x+64}

\newline

Compare degrees: To find the horizontal asymptotes of a rational function, we need to compare the degrees of the numerator and the denominator. If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is $y = 0$ .
Identify numerator degree: The degree of the numerator, which is the highest power of $x$ in the numerator, is $1$ (since the numerator is $x-4$ ).
Identify denominator degree: The degree of the denominator, which is the highest power of $x$ in the denominator, is $2$ (since the denominator is $10x^2-56x+64$ ).
Determine horizontal asymptote: Since the degree of the numerator $1$ is less than the degree of the denominator $2$ , the horizontal asymptote of the function is $y = 0$ .
Final result: Therefore, the function $f(x) = \frac{x-4}{10x^2-56x+64}$ has one horizontal asymptote, which is $y = 0$ .

More problems from Find the roots of factored polynomials

Question

Find the degree of this polynomial.

\newline

`5b^{10} + 3b^3`

\newline

Posted 5 months ago

Question

\newline

(9a + 5) - (2a + 4)

\newline

Posted 5 months ago

Question

Find the product. Simplify your answer.

\newline

-3v^2(v^2 - 9)

\newline

Posted 5 months ago

Question

Find the product. Simplify your answer.

\newline

(v - 3)(4v + 1)

\newline

Posted 5 months ago

Question

Find the square. Simplify your answer.

\newline

(3y + 2)^2

\newline

Posted 5 months ago

Question

Divide. If there is a remainder, include it as a simplified fraction.

\newline

(24t^2 + 36t) \div 6t

\newline

Posted 5 months ago

Question

Is the function

q(x) = x^6 - 9

even, odd, or neither?

\newline

\newline

\text{[[even][odd][neither]]}

Posted 9 months ago

Question

Find the product. Simplify your answer.

\newline

-3q^2(-3q^2 + q)

\newline

Posted 9 months ago

Question

Find the product. Simplify your answer.

\newline

(r + 3)(4r + 2)

\newline

Posted 9 months ago

Question

Find the roots of the factored polynomial.

\newline

(x + 7)(x + 4)

\newline

Write your answer as a list of values separated by commas.

\newline

x =

Posted 9 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant