Full solution
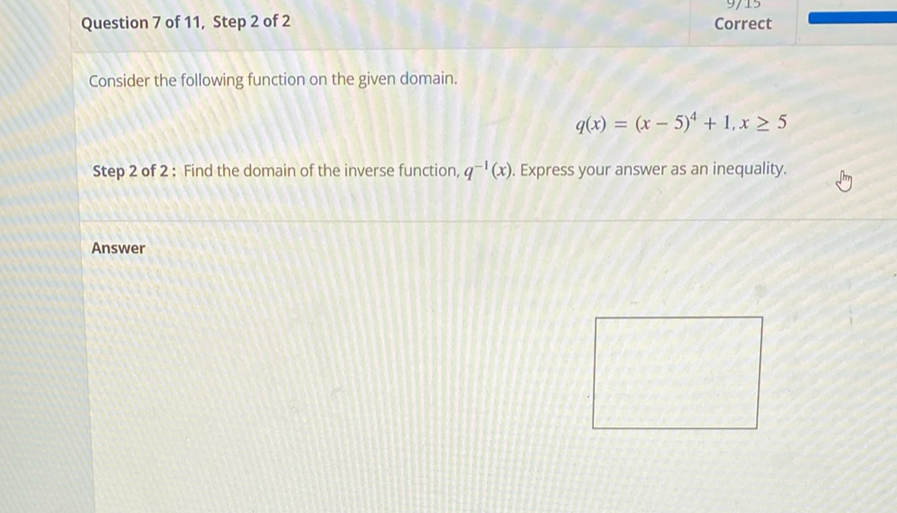
Q. Consider the following function on the given domain.
- Understand function and domain: Understand the function and its domain.The function is defined for . This means that the smallest value can take is , and there is no upper limit to the values of . Since the function involves raising to the fourth power, the output will always be positive or zero (when ), and then is added, making the minimum output value . Therefore, the range of is .
- Determine inverse function domain: Determine the domain of the inverse function.The domain of the inverse function is the range of the original function . Since we have established that the range of is , the domain of will be the same.
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help