Full solution
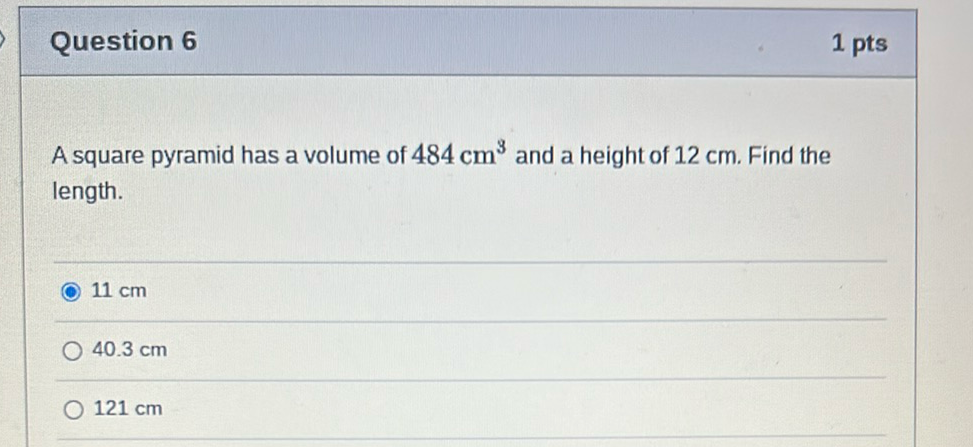
Q. Question ptsA square pyramid has a volume of and a height of . Find the length.
- Identify Formula: Identify the formula for the volume of a square pyramid.Volume = Here, the base area is the area of the square base, which can be calculated as side length squared .So, Volume = Given: Volume = , height = We need to find the side length .
- Substitute and Solve: Substitute the given values into the volume formula and solve for . To isolate , multiply both sides by and divide by .
- Calculate : Calculate the value of .
- Find Side Length: Find the side length by taking the square root of .
More problems from Volume of cubes and rectangular prisms: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help