AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
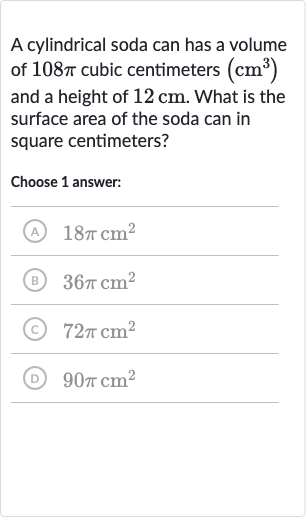
A cylindrical soda can has a volume of and a height of . What is the surface area of the soda can in square centimeters?Choose answer:(A) (B) (C) (D)
Full solution
Q. A cylindrical soda can has a volume of and a height of . What is the surface area of the soda can in square centimeters?Choose answer:(A) (B) (C) (D)
- Identify Given Information: Identify the given information and the formula for the volume of a cylinder.Volume of a cylinder = , where is the radius and is the height.Given: and .We need to find the radius of the cylinder first.
- Use Volume Formula: Use the volume formula to solve for the radius.Divide both sides by to simplify.
- Solve for Radius: Divide both sides by to isolate .
- Find Surface Area Formula: Take the square root of both sides to solve for .Now we have the radius of the cylinder.
- Substitute Values: Identify the formula for the surface area of a cylinder.Surface area , where is the surface area, is the radius, and is the height.We have cm and cm.
- Combine Terms: Substitute the values of and into the surface area formula.
- Combine Terms: Substitute the values of and into the surface area formula.Combine the terms to find the total surface area.The surface area of the soda can is square centimeters.
More problems from Volume of cubes and rectangular prisms: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
