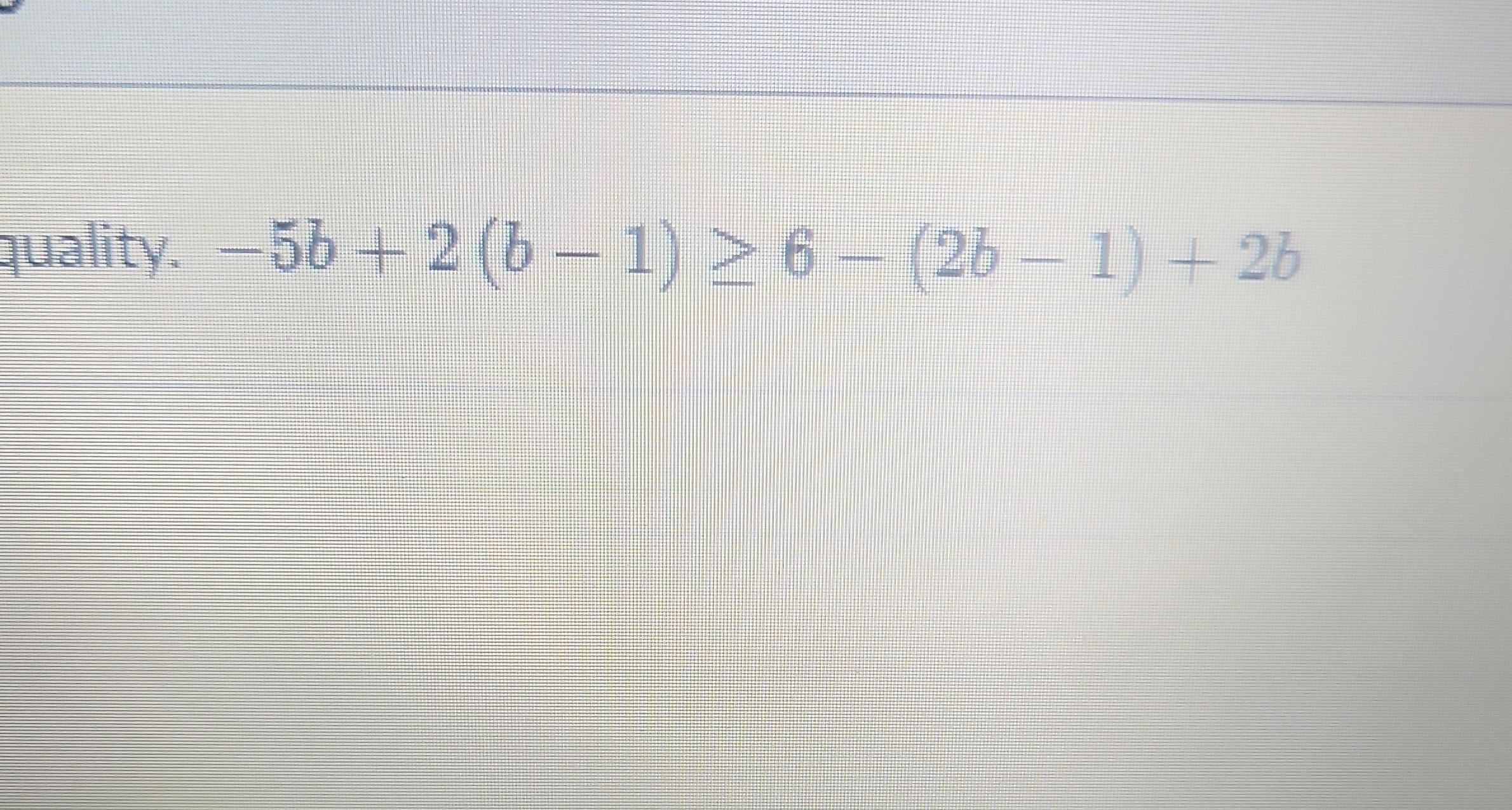AI tutor
Full solution
Q.
- Distribute : Distribute the into the parentheses on the left side of the inequality.
- Distribute negative sign: Distribute the negative sign into the parentheses on the right side of the inequality.
- Combine like terms: Combine like terms on both sides of the inequality.Left side: Right side:
- Write simplified inequality: Write the simplified inequality.
- Add to isolate: Add to both sides of the inequality to isolate the term with the variable .
- Divide to solve for b: Divide both sides of the inequality by to solve for . Remember that dividing by a negative number reverses the inequality sign.
More problems from Solve multi-step equations with fractional coefficients
QuestionGet tutor help